题目内容
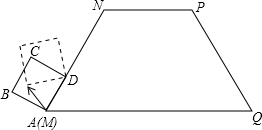 如图,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°.正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动,求正方形在整个翻滚过程中点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S=( )
如图,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°.正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动,求正方形在整个翻滚过程中点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S=( )分析:先根据点A绕点D翻滚,然后绕点C翻滚,然后绕点B翻滚,半径分别为1、2、1,翻转角分别为90°、90°、150°,据此画出图形.再结合总结的翻转角度和翻转半径,求出圆弧与梯形的边长围成的扇形的面积即可.
解答: 解:(1)作图如图;
解:(1)作图如图;
(2)∵点A绕点D翻滚,然后绕点C翻滚,然后绕点B翻滚,半径分别为1、
、1,翻转角分别为90°、90°、150°,
∴S=2×
+2×
+2×
+4×
×12
=
+π+
π+2
=
+2.
故选A.
 解:(1)作图如图;
解:(1)作图如图;(2)∵点A绕点D翻滚,然后绕点C翻滚,然后绕点B翻滚,半径分别为1、
| 2 |
∴S=2×
| 90×1×π |
| 360 |
90π×(
| ||
| 360 |
| 150π×1 |
| 360 |
| 1 |
| 2 |
=
| π |
| 2 |
| 5 |
| 6 |
=
| 7π |
| 3 |
故选A.
点评:本题考查了扇形面积的计算、等腰梯形的性质、旋转的性质,作出图形并熟悉扇形面积是解题的关键.

练习册系列答案
相关题目
 如图,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°.正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动.正方形在整个翻滚过程中点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S是
如图,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°.正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动.正方形在整个翻滚过程中点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S是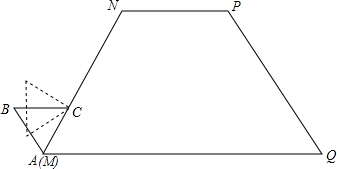 翻滚到有一个顶点与Q重合即停止滚动.
翻滚到有一个顶点与Q重合即停止滚动.