题目内容
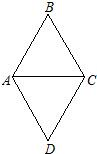如图，对于△ABC、△ADC均为边长为6的等边三角形，（1）四边形是什么四边形？请说明理由；
（2）建立适当的直角坐标系，写出各顶点的坐标．
分析：（1）考查菱形的判定，由各边相等可知其为菱形，
（2）以A为原点建立直角坐标系，进而求出各点的坐标．
（2）以A为原点建立直角坐标系，进而求出各点的坐标．
解答：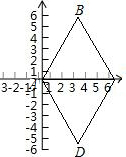
解：（1）四边形是菱形，
理由：△ABC、△ADC均为等边三角形，且以AC为公共边，则四边形ABCD的各边相等，所以其为菱形．
（2）如图所示，以A为原点建立直角坐标系，
∵△ABC与△ACD均为等边三角形，
∴结合图形可得A点坐标（0，0），B点坐标（3，3
），C点坐标（6，0），D点坐标（3，-3
）．
解：（1）四边形是菱形，理由：△ABC、△ADC均为等边三角形，且以AC为公共边，则四边形ABCD的各边相等，所以其为菱形．
（2）如图所示，以A为原点建立直角坐标系，
∵△ABC与△ACD均为等边三角形，
∴结合图形可得A点坐标（0，0），B点坐标（3，3
| 3 |
| 3 |
点评：熟练掌握菱形的性质及判定定理，会画简单的直角坐标系．
练习册系列答案
相关题目
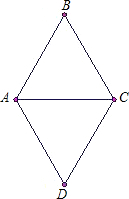如图，对于△ABC、△ADC均为边长为6的等边三角形，建立适当的直角坐标系．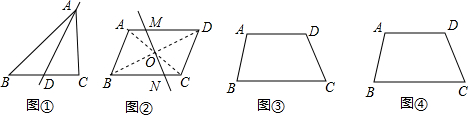
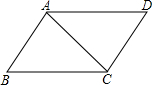如图，如果△ABC≌△CDA，∠BAC=∠DCA，∠B=∠D，对于以下结论：
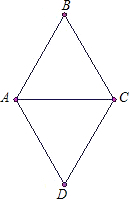如图，对于△ABC、△ADC均为边长为6的等边三角形，建立适当的直角坐标系．