题目内容
已知,如图,A、B、C三个村庄在一条东西走向的公路沿线上,AB=12千米,在B村的正北方向有一个D村,测得∠DAB=45°,∠DCB=28°,今将△ACD区域进行规划,除其中面积为0.5平方千米的水塘外,准备把剩 余的一半作为绿化用地.
余的一半作为绿化用地.
(1)求BC的长.
(2)求绿化地的面积.
(结果精确到0.1,sin28°=0.4695,sin62°=0.8829,tan28°=0.5317,tan62°=1.8808)
 余的一半作为绿化用地.
余的一半作为绿化用地.(1)求BC的长.
(2)求绿化地的面积.
(结果精确到0.1,sin28°=0.4695,sin62°=0.8829,tan28°=0.5317,tan62°=1.8808)
分析:(1)在Rt△ABD中,由∠DAB=45°,可得出∠BDA=45°,故DB=AB=12,在Rt△BCD中利用锐角三角函数的定义即可求出BC的长;
(2)根据S绿化地=S△ACD-S池塘
[
(AC+BD)×12-0.5]即可得出结论.
(2)根据S绿化地=S△ACD-S池塘
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)在Rt△ABD中,
∵∠DAB=45°,
∴∠BDA=45°,
∴DB=AB=12,
在Rt△BCD中,
∵tan∠BDC=
,
∴BC=BDtan∠BDC=12×tan62°=22.6(千米);
(2)S绿化地=
[
(AC+BD)×12-0.5]
=
[
×(22.57+12)×12-0.5]
=103.5(平方千米)
∵∠DAB=45°,
∴∠BDA=45°,
∴DB=AB=12,
在Rt△BCD中,
∵tan∠BDC=
| BC |
| BD |
∴BC=BDtan∠BDC=12×tan62°=22.6(千米);
(2)S绿化地=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=103.5(平方千米)
点评:本题考查的是解直角三角形的应用,涉及到锐角三角函数的定义、等腰直角三角形的判定与性质及三角形的面积公式,涉及面较广,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,测得C在B的北偏西45°方向上.
,测得C在B的北偏西45°方向上. 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为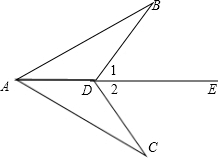 已知,如图,∠1=∠2,
已知,如图,∠1=∠2, 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为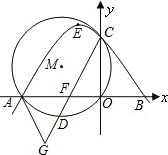 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧