题目内容
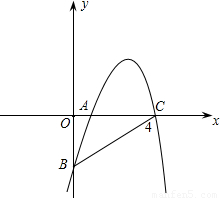
 如图抛物线y=-x2+3x-1-a2与x轴正半轴相交于两点,点A在点B的左侧,其中A(x1,0)、B(x2,0).当x=x2-3时,y
如图抛物线y=-x2+3x-1-a2与x轴正半轴相交于两点,点A在点B的左侧,其中A(x1,0)、B(x2,0).当x=x2-3时,y<
<
0(填“>”“=”或“<”号).分析:先由二次函数的性质可知抛物线y=-x2+3x-1-a2与x轴相交于点A(x1,0)、B(x2,0),则一元二次方程-x2+3x-1-a2=0的两根为x1,x2,由根与系数的关系求得x1+x2=3,即x=x2-3=-x1<0,则当x=x2-3时,y小于0.
解答:解:∵抛物线y=-x2+3x-1-a2与x轴相交于点A(x1,0)、B(x2,0),
∴一元二次方程-x2+3x-1-a2=0的两根为x1,x2,
∴x1+x2=3,
∴x1=3-x2,
∵抛物线y=-x2+3x-1-a2与x轴正半轴相交于两点,
∴x1>0,x2>0,
∴x=x2-3=-x1<0,
由图象可知,此时y<0.
故答案为<.
∴一元二次方程-x2+3x-1-a2=0的两根为x1,x2,
∴x1+x2=3,
∴x1=3-x2,
∵抛物线y=-x2+3x-1-a2与x轴正半轴相交于两点,
∴x1>0,x2>0,
∴x=x2-3=-x1<0,
由图象可知,此时y<0.
故答案为<.
点评:本题考查了二次函数图象的性质,二次函数与一元二次方程的关系,韦达定理,由根与系数的关系得到x=x2-3=-x1,是解题的关键.

练习册系列答案
相关题目
 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.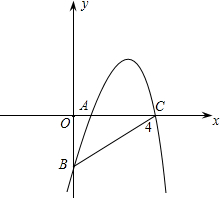 如图抛物线y=-x2+5x+k经过点C(4,0)与x轴交于另一点A,与y轴交于点B.
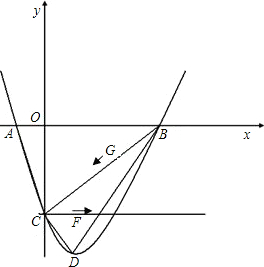
如图抛物线y=-x2+5x+k经过点C(4,0)与x轴交于另一点A,与y轴交于点B.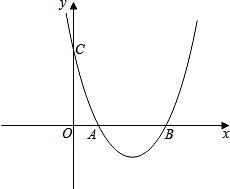 如图抛物线y=x2-(a+1)x+a交x轴于A(1,0)、B两点,交y轴于C点.
如图抛物线y=x2-(a+1)x+a交x轴于A(1,0)、B两点,交y轴于C点.