题目内容
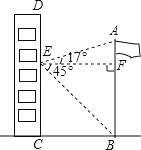
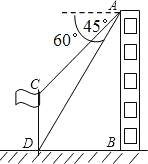
【题目】在20m高的楼AB的前方有一个旗杆CD,从楼的顶端A测得旗杆的顶端C的俯角为45°,底端D的俯角为60°.
(1)求旗杆的底端D与楼的底端B的距离;
(2)求旗杆CD的高度.
[说明:(1)(2)的计算结果精确到0.01m.参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732].
≈1.732].
【答案】(1)旗杆的底端D与楼的底端B的距离约为11.55m;(2)旗杆CD的高度约为8.45m.
【解析】
试题分析:(1)在Rt△ABD中,利用AB的长和∠DAB的度数求得DB的值即为旗杆的底端D与楼的底端B的距离;
(2)作CE⊥AB与E点,利用两平行线之间的距离相等得到CE=DB,在直角三角形ACE中求得AE后,用AB减去AE即可得到旗杆的高度.
试题解析:(1)由题意可知,∠DAB=30°,
在Rt△ADB中,DB=ABtan30°,
=20×![]() ,
,
≈20×![]() ,
,
≈11.55,
答:旗杆的底端D与楼的底端B的距离约为11.55m;
(2)作CE⊥AB,垂足为E,

则四边形CDBE为矩形.
∴CE=DB,CD=EB,
在Rt△ACE中,∠CAE=45°,AE=CE=DB=![]() ,
,
∴CD=EB=AB-AE,
=20-![]() ≈20-
≈20-![]() ,
,
≈8.45.
答:旗杆CD的高度约为8.45m.

练习册系列答案
相关题目