题目内容
(2012•龙岩质检)1979年全国人大通过决定,每年3月12日是我国植树节;今年某校计划购买甲、乙两种树苗共2000株绿化校园,已知甲种树苗每株2元,乙种树苗每株3元.
(1)若购买这批树苗共用了4500元,求甲、乙两种树苗各购买了多少株?
(2)若购买这批树苗的钱不超过4700元,问应选购甲种树苗至少多少株?
(3)相关资料表明:甲、乙两种树苗的成活率分别为94%和99%,若要使这批树苗的成活率不低于96%且买树苗的总费用最小,问应选购甲、乙两种树苗各多少株?总费用最小是多少元?
(1)若购买这批树苗共用了4500元,求甲、乙两种树苗各购买了多少株?
(2)若购买这批树苗的钱不超过4700元,问应选购甲种树苗至少多少株?
(3)相关资料表明:甲、乙两种树苗的成活率分别为94%和99%,若要使这批树苗的成活率不低于96%且买树苗的总费用最小,问应选购甲、乙两种树苗各多少株?总费用最小是多少元?
分析:(1)设购买甲种树苗x株,然后表示出乙种树苗的株数,再根据甲乙两种树苗的钱数的和等于总钱数列出方程求解即可;
(2)根据甲乙两种树苗的钱数的和不大于4700元,列出不等式求解即可;
(3)表示出购买这批树苗的总费用与甲种树苗的株数的关系式,再根据成活率不低于96%列出不等式求出x的取值范围,然后根据一次函数的增减性解答.
(2)根据甲乙两种树苗的钱数的和不大于4700元,列出不等式求解即可;
(3)表示出购买这批树苗的总费用与甲种树苗的株数的关系式,再根据成活率不低于96%列出不等式求出x的取值范围,然后根据一次函数的增减性解答.
解答:解:设购买甲种树苗x株,则购买乙种树苗(2000-x)株,
(1)根据题意得,2x+3(2000-x)=4500,
解这个方程得,x=1500,
2000-x=2000-1500=500,
即:购买甲种树苗1500株,乙种树苗500株;
(2)根据题意得,2x+3(2000-x)≤4700,
解得x≥1300,
即选购甲种树苗至少为1300株;
(3)设购买这批树苗总费用为y元,
根据题意得,y=2x+3(2000-x)=-x+6000,
又由题意可得,94%x+99%(2000-x)≥2000×96%,
解得x≤1200,
∵k=-1<0,
∴一次函数的函数值y随x增大而减小,
∴当x=1200时,y最小=-1200+6000=4800,
此时,乙种树苗为2000-1200=800株,
即:购买甲种树苗为1200株,乙种树苗为800株,总费用y最小为4800元.
(1)根据题意得,2x+3(2000-x)=4500,
解这个方程得,x=1500,
2000-x=2000-1500=500,
即:购买甲种树苗1500株,乙种树苗500株;
(2)根据题意得,2x+3(2000-x)≤4700,
解得x≥1300,
即选购甲种树苗至少为1300株;
(3)设购买这批树苗总费用为y元,
根据题意得,y=2x+3(2000-x)=-x+6000,
又由题意可得,94%x+99%(2000-x)≥2000×96%,
解得x≤1200,
∵k=-1<0,
∴一次函数的函数值y随x增大而减小,
∴当x=1200时,y最小=-1200+6000=4800,
此时,乙种树苗为2000-1200=800株,
即:购买甲种树苗为1200株,乙种树苗为800株,总费用y最小为4800元.
点评:本题考查了一次函数的应用,一元一次方程的应用,一元一次不等式的应用,明确不等关系的语句“不超过”“不低于”的含义,然后准确列出不等式是解题的关键,(3)题型整理出一次函数关系,然后根据不等关系求出自变量的取值范围,再根据一次函数的增减性求解是常用的方法,一定要熟练掌握并灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
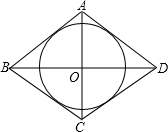 (2012•龙岩质检)如图,菱形ABCD中,若AC=6,BD=8,则该菱形的内切圆半径r=
(2012•龙岩质检)如图,菱形ABCD中,若AC=6,BD=8,则该菱形的内切圆半径r=