Question

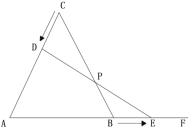
【题目】等边三角形的边长为，点从点出发沿向运动，点从出发沿的延长线向右运动，已知点都以每秒的速度同时开始运动，运动过程中与相交于点．

（1）运动几秒后，为直角三角形？

（2）求证：在运动过程中，点始终为线段的中点．

Answer 1

【答案】（1） （2）见解析

【解析】

（1）设x秒时，△ADE为直角三角形，则CD＝0.5x，BE＝0.5x，AD＝40.5x，AE＝4＋0.5x，根据30°的直角边＝斜边的一般建立方程求出其解即可；

（2）作DG∥AB交BC于点E，证明△DGP≌△EBP，就可以得出PD＝PE．

（1）∵△ABC是等边三角形，

∴AB＝BC＝AC＝4cm，∠A＝∠ABC＝∠C＝60°．

设x秒时，△ADE为直角三角形，

∴∠ADE＝90°，CD＝0.5x，BE＝0.5x，AD＝40.5x，AE＝4＋0.5x，

∴∠AED＝30°，

∴AE＝2AD，

∴4＋0.5x＝2（40.5x），

∴x＝；

答：运动秒后，△ADE为直角三角形；

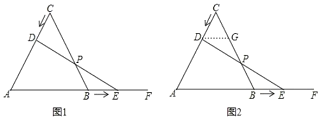
（2）作DG∥AB交BC于点G，

∴∠GDP＝∠BEP，∠DGP＝∠EBP，∠CDG＝∠A＝60°，∠CGD＝∠ABC＝60°，

∴∠C＝∠CDG＝∠CGD，

∴△CDG是等边三角形，

∴DG＝DC，

∵DC＝BE，

∴DG＝BE．

在△DGP和△EBP中

，

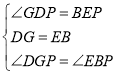∴△DGP≌△EBP（ASA），

∴DP＝PE．

∴在运动过程中，点P始终为线段DE的中点．