题目内容
【题目】课堂上,数学老师提出了如下问题:
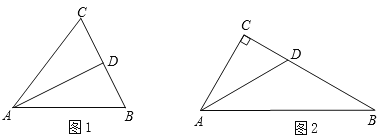
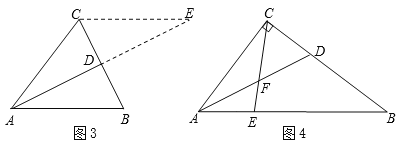
如图1,若线段AD为△ABC的角平分线,请问![]() 一定成立吗?
一定成立吗?
小明和小芳分别作了如下探究:
小明发现:如图2,当△ABC为直角三角形时,且∠C=90°,∠CAB=60°时,结论成立;
小芳发现:如图3,当△ABC为任意三角形时,过点C作AB的平行线,交AD的延长线于点E,利用此图可以证明![]() 成立.
成立.
【答案】(1)(2)(3)
【解析】试题分析:(1)设CD的长为a,Rt△CAB中,由角平分线的定义,可得∠B= 30°,由正切定义可得AC、AB、CB以及DB的长,即可得证;
(2)由两直线平行,内错角相等可得∠E=∠EAB,∠B=∠ECB,即可证明△CED∽△BAD,由相似三角形的性质得出![]() ,由等角对等边得出CE=CA,即可得证.
,由等角对等边得出CE=CA,即可得证.
试题解析:(1)设CD的长为a,
Rt△CAB中,∠CAB=60°,AD平分∠CAB,
∴∠B=∠CAD=∠DAB= 30°,



∴DB=BC-CD=3a-a=2a
∴![]()
(2)∵CE∥AB,
∴∠E=∠EAB,∠B=∠ECB,
∴△CED∽△BAD,
∴![]() ,
,
∵∠E=∠EAB,∠EAB=∠CAD,
∴∠E=∠CAD
∴CE=CA
∴![]() ,
,

练习册系列答案
相关题目
【题目】商场销售某种冰箱,该种冰箱每台进价为2500元.已知原销售价为每台2900元时,平均每天能售出8台.若在原销售价的基础上每台降价50元,则平均每天可多售出4台.设每台冰箱的实际售价比原销售价降低了x元.
(1)填表(不需化简):
每天的销售量/台 | 每台销售利润/元 | |
降价前 | 8 | 400 |
降价后 |
(2)商场为使这种冰箱平均每天的销售利润达到5000元,则每台冰箱的实际售价应定为多少元?