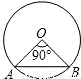
题目内容
(2010•宣城二模)2010年4月底,全新帐蓬厂接受一批支援青海玉树灾区抗震帐蓬的生产任务.根据要求,帐蓬的一个横截面由等腰三角形和矩形组成(如图所示),已知等腰△ABE的底角∠ABE=a,且tan a= ,矩形的边CD=2BC,这个横截面的框架(包括BE)的所用钢管总长为16m,求帐蓬顶A到底部CD的距离(结果精确到0.1m).
,矩形的边CD=2BC,这个横截面的框架(包括BE)的所用钢管总长为16m,求帐蓬顶A到底部CD的距离(结果精确到0.1m).
【答案】分析:有框架的周长已知,通过等腰三角形ABE,α的正切值,设了AG,BG的长,得到的等式可解得a的值,从而得到AF的值.
解答: 解:过A点作AF⊥CD于F点,交BE于G点,则AG⊥BE
解:过A点作AF⊥CD于F点,交BE于G点,则AG⊥BE
又∵AB=AE
∴BE=2BG(2分)
在Rt△ABG中,tanα=
设AG=3a,BG=4a
∴CD=BE=8a,BC=DE=GF=4a(5分)
根据勾股定理,AB=AE= (6分)
(6分)
∴2(5a+4a+8a)=16
解得a= (8分)
(8分)
∴AF=AG+FG= cm(9分)
cm(9分)
答:帐篷的点A到底CD的距离即AF大约3.3cm(10分)
点评:本题把三角函数的概念在里面,以框架的总长为线索,设出AG为3a,BG为4a,列式从而求得a的值,进一步从而求得AF的值.
解答:
 解:过A点作AF⊥CD于F点,交BE于G点,则AG⊥BE
解:过A点作AF⊥CD于F点,交BE于G点,则AG⊥BE又∵AB=AE
∴BE=2BG(2分)
在Rt△ABG中,tanα=

设AG=3a,BG=4a
∴CD=BE=8a,BC=DE=GF=4a(5分)
根据勾股定理,AB=AE=
 (6分)
(6分)∴2(5a+4a+8a)=16
解得a=
 (8分)
(8分)∴AF=AG+FG=
 cm(9分)
cm(9分)答:帐篷的点A到底CD的距离即AF大约3.3cm(10分)
点评:本题把三角函数的概念在里面,以框架的总长为线索,设出AG为3a,BG为4a,列式从而求得a的值,进一步从而求得AF的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 m,与篮框中心的水平距离是7m,已知篮球的运动轨迹是抛物线,篮框距地面3m.
m,与篮框中心的水平距离是7m,已知篮球的运动轨迹是抛物线,篮框距地面3m.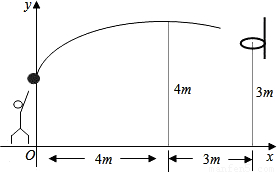
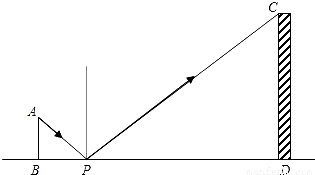
 ;
; =1.41,
=1.41, =1.73,结果保留整数).
=1.73,结果保留整数).