题目内容
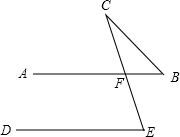 如图,直线AB∥DE,∠E=64°,则∠B+∠C=
如图,直线AB∥DE,∠E=64°,则∠B+∠C=
- A.136°
- B.116°
- C.36°
- D.64°
D
分析:先根据两直线平行,同位角相等的性质求出∠AFC的度数,再根据三角形的一个外角等于与它不相邻的两个内角的和进行解答.
解答:∵AB∥DE,∠E=64°,
∴∠AFC=∠E=64°,
在△BCF中,∠B+∠C=∠AFC=64°.
故选D.
点评:本题考查了两直线平行,同位角相等的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.
分析:先根据两直线平行,同位角相等的性质求出∠AFC的度数,再根据三角形的一个外角等于与它不相邻的两个内角的和进行解答.
解答:∵AB∥DE,∠E=64°,
∴∠AFC=∠E=64°,
在△BCF中,∠B+∠C=∠AFC=64°.
故选D.
点评:本题考查了两直线平行,同位角相等的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.

练习册系列答案
相关题目
 8、如图,直线AB∥DE,BC⊥CD,若∠1=25°,则∠2的度数是
8、如图,直线AB∥DE,BC⊥CD,若∠1=25°,则∠2的度数是
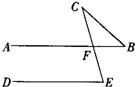 如图,直线AB∥DE,∠E=64°,则∠B+∠C=( )
如图,直线AB∥DE,∠E=64°,则∠B+∠C=( )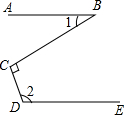 如图,直线AB∥DE,BC⊥CD,若∠1=25°,则∠2的度数是________.
如图,直线AB∥DE,BC⊥CD,若∠1=25°,则∠2的度数是________.
