Question

8、如图，直线AB∥DE，BC⊥CD，若∠1=25°，则∠2的度数是

115°

．

Answer 1

分析：过C作CM∥AB，根据平行公理得到CM∥AB∥DE，由∠1的度数能求出∠BCM的度数，由BC⊥CD，进一步求出∠MCD的度数，根据平行线的性质（同旁内角互补）即可求出∠2的度数，即得到答案．

解答：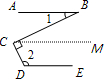
解：过C作CM∥AB，
∵AB∥DE，
∴CM∥AB∥DE，
∴∠1=∠BCM，
∵∠1=25°，
∴∠BCM=25°，
∵BC⊥CD，
∴∠BCD=90°，
∴∠MCD=90°-25°=65°，
∵CM∥DE，
∴∠2+∠MCD=180°，
∴∠2=180°-65°=115°，
故答案为：115°．

点评：本题主要考查了平行线的性质，平行公理和及推论，垂直的定义等知识点，作辅助线后能求出各个角的度数是解此题的关键．