��Ŀ����
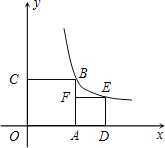
����Ŀ����ͼ����֪��A��4��0����B��0��4![]() ������һ��ֱ�����dz�DEF������OAB�ڣ�ʹ��б��FD���߶�AB�ϣ����dz߿������߶�AB���»�����������EFD=30����ED=2����GΪ��FD���е㣮
������һ��ֱ�����dz�DEF������OAB�ڣ�ʹ��б��FD���߶�AB�ϣ����dz߿������߶�AB���»�����������EFD=30����ED=2����GΪ��FD���е㣮
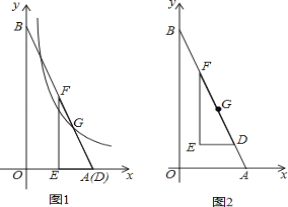
��1����ֱ��AB�Ľ���ʽ��
��2����ͼ1������D���A�غ�ʱ������G�ķ���������y=![]() ��k��0���Ľ���ʽ��
��k��0���Ľ���ʽ��
��3�������dz����Ĺ����У�������G�ķ�����������ͼ���ܷ�ͬʱ������F������ܣ������ʱ�����������Ľ���ʽ��������ܣ�˵�����ɣ�
���𰸡���1��y=-![]() x+4
x+4![]() ����2��y=
����2��y=![]() ����3��y=
����3��y=![]() ��
��
��������
�����������1����ֱ��AB�Ľ���ʽΪy=kx+b���ѵ�A��B��������룬��ɷ����飬�ⷽ�������k��b��ֵ���ɣ�
��2����Rt��DEF�У����EF��DF���������D���꣬�ó���F��G���꣬�ѵ�G������뷴�����������k���ɣ�
��3����F��t��-![]() t+4
t+4![]() �����ó�D��G���꣬�����G��F�ķ�������������ʽΪy=
�����ó�D��G���꣬�����G��F�ķ�������������ʽΪy=![]() ���ô���ϵ�������t��m�����ɵó���������������ʽ��
���ô���ϵ�������t��m�����ɵó���������������ʽ��
�����������1����ֱ��AB�Ľ���ʽΪy=kx+b��
��A��4��0����B��0��4![]() ����
����
��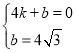 ��
��
��ã�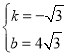 ��
��
��ֱ��AB�Ľ���ʽΪ��y=-![]() x+4
x+4![]() ��
��
��2������Rt��DEF����EFD=30����ED=2��
��EF=2![]() ��DF=4��
��DF=4��
����D���A�غϣ�
��D��4��0����
��F��2��2![]() ����
����
��G��3��![]() ����
����
������������y=![]() ������G��
������G��
��k=3![]() ��
��
�������������Ľ���ʽΪ��y=![]() ��
��
��3��������G�ķ�����������ͼ����ͬʱ������F���������£�
����F��ֱ��AB�ϣ�
����F��t��-![]() t+4
t+4![]() ����
����
����ED=2��
��D��t+2��-![]() t+2
t+2![]() ����
����
����GΪ��FD���е㣮
��G��t+1��-![]() t+3
t+3![]() ����
����
������G�ķ�����������ͼ��Ҳ������F��
�����ʽΪy=![]() ��
��
��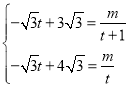 ��
��
�������-![]() t+3
t+3![]() ����t+1��=��-
����t+1��=��-![]() t+4
t+4![]() ��t��
��t��
��ã�t=![]() ��
��
��m=![]() ��
��
��������G�ķ�����������ͼ����ͬʱ������F�������������������ʽΪ��y=![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�