题目内容
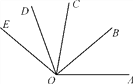
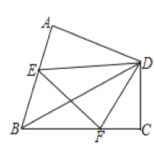
【题目】如图,在四边形ABCD中,∠A=∠C=90°,∠B=α,在AB,BC上分别找一点E,F,使△DEF的周长最小,此时,∠EDF=______。(用含α的代数式表示)
【答案】180°2α
【解析】
根据要使△DEF的周长最小,即利用点的对称,使三角形的三边在同一直线上,作出D关于AB和BC的对称点P,Q,结合四边形的内角和即可得出答案。
如图,作点D关于BA的对称点P,点D关于BC的对称点Q,连接PQ,交AB于E,交BC于F,则点E,F即为所求。
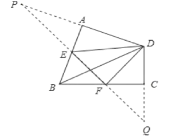
∵四边形ABCD中,∠A=∠C=90°,∠B=α,
∴∠PDQ=180°α,
在三角形PDQ中,∠P+∠Q=180°-∠PDQ =α,
∵点P与点D关于AB对称,点D与点Q关于DQ对称,
∴∠P=∠ADE,∠Q=∠FDQ
∴∠ADE+ FDQ=∠P+∠Q=α
∴∠EDF=∠PDQ-(∠ADE+ ∠FDQ)=180°2α

练习册系列答案
相关题目
【题目】某市在今年对全市6000名八年级学生进行了一次视力抽样调查,并根据统计数据,制作了的统计表和如图所示统计图.
组别 | 视力 | 频数(人) |
A |
| 20 |
B |
| a |
C |
| b |
D |
| 70 |
E |
| 10 |
请根据图表信息回答下列问题:
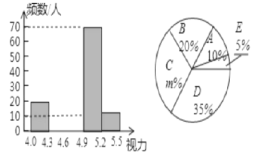
(1)求抽样调查的人数;
(2)![]() ______,
______,![]() ______,
______,![]() ______;
______;
(3)补全频数分布直方图;
(4)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是多少?根据上述信息估计该市今年八年级的学生视力正常的学生大约有多少人?