题目内容
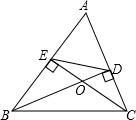
如图，已知BD、CE都是△ABC的高，CE交BD于O，
（1）请你写出图中的相似三角形；
（2）从中挑选其中的一对进行证明．
解：（1）图中相似三角形有：△ABC∽△ADE，△DOC∽△EOB，△ABD∽△ACE，△DOE∽△COB．
（2）证明：根据三角形的面积公式得：AD×AC=AE×AB，
则AD：AB=AE：AC，
∵∠A=∠A，
∴△ABC∽△ADE（一组对应角相等，两组夹边对应成比例）．
分析：（1）根据相似三角形的判定定理求出即可；
（2）根据三角形的面积公式推出AD：AB=AE：AC，即可求出答案．
点评：本题主要考查对相似三角形的判定，三角形的面积等知识点的理解和掌握，能熟练地运用相似三角形的判定定理进行推理是解此题的关键．
练习册系列答案
全优点练单元计划系列答案
相关题目
22、如图，已知BD、CE都是△ABC的高，
如图，已知BD、CE都是△ABC的高．
如图，已知BD、CE是△ABC的高，下面给出四个结论：①∠1=∠2=90°-∠A；②∠3=∠A=90°-∠1；③∠BOC=∠A+∠1+∠2；④∠1+∠2+∠3+∠A=180°，其中正确的个数是（ ）
如图，已知BD，CE为△ABC的角平分线，F为DE的中点，点F到AC，AB，BC的距离分别为FG=a，FH=b．FM=c，若c2-c-2ab+