题目内容
如图，OC是∠AOB的平分线，PD⊥DA于点D，PD=2，则P点到OB的距离是
- A.1
- B.2
- C.3
- D.4
B
分析：可过点P作PE⊥OB，由角平分线的性质可得，PD=PE，进而可得出结论．
解答：
解：如图，过点P作PE⊥OB，
∵OC是∠AOB的平分线，点P在OC上，且PD⊥OA，PE⊥OB，
∴PE=PD，又PD=2，
∴PE=PD=2．
故选B．
点评：本题考查了角平分线的性质；要熟练掌握角平分线的性质，即角平分线上的点到角两边的距离相等．
分析：可过点P作PE⊥OB，由角平分线的性质可得，PD=PE，进而可得出结论．
解答：
解：如图，过点P作PE⊥OB，∵OC是∠AOB的平分线，点P在OC上，且PD⊥OA，PE⊥OB，
∴PE=PD，又PD=2，
∴PE=PD=2．
故选B．
点评：本题考查了角平分线的性质；要熟练掌握角平分线的性质，即角平分线上的点到角两边的距离相等．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
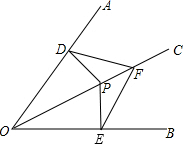
13、如图，OC是∠AOB的平分线，点D是OC上的一点，DE⊥OA于点E，DF⊥OB于点F，连接EF，交OC于点P，把这个图形沿OC对折后观察，除∠AOC=∠BOC外，你还可以发现的结论是
22、（1）画出下图的三视图．
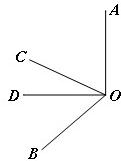25、如图，OC是∠AOB的平分线，且∠AOD=90°．
如图，OC是∠AOB的平分线，OD是∠BOC的平分线，那么下列各式中正确的是（ ）A、∠COD=
| ||
B、∠AOD=
| ||
C、∠BOD=
| ||
D、∠BOC=
|