题目内容
【题目】已知,在![]() 中,
中,![]() ,
,![]() 是
是![]() 边上的一个动点,将
边上的一个动点,将![]() 沿
沿![]() 所在直线折叠,使点
所在直线折叠,使点![]() 落在点
落在点![]() 处.
处.
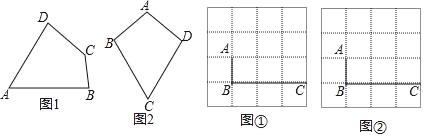
(1)如图①,若点![]() 是
是![]() 的中点,连接
的中点,连接![]() .求证:四边形
.求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图②,若![]() ,求
,求![]() 的值.
的值.
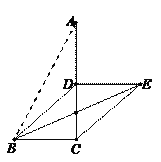
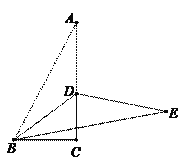
图① 图②
【答案】(1)见解析(2) ![]()
【解析】分析:(1)证明DE∥BC,DE=BC即可;
(2) 如图,作DF⊥AB于F,EM⊥AC于M,延长BD交EA于G.设BD=AD=x,则CD=8-x,在Rt△BDC中,可得x2=(8-x)2+42,推出x=5,在![]() 中,
中,![]() ,故
,故![]() ,由
,由![]() ,得
,得![]() ,由
,由![]() ∽
∽![]() ,可得
,可得![]() ,由此求出AE,由
,由此求出AE,由![]() ∽
∽![]() ,可得
,可得![]() ,由此求出AM,可得MC , 易证四边形
,由此求出AM,可得MC , 易证四边形![]() 是矩形,由此即可解决问题.
是矩形,由此即可解决问题.
详解:(1)证明:在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,
∴![]()
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() .
.
由折叠得:![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴四边形![]() 是平行四边形;
是平行四边形;
(2)如图

连接![]() ,分别过点
,分别过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,则
,则![]() 为等腰三角形,
为等腰三角形,![]() .
.
设![]() ,则
,则![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]()
![]() ,
,
由![]() ∽
∽![]() ,可得
,可得![]() ,
,
∴![]()
∴![]() ,又
,又![]() .
.
∴![]() ,
,
由![]() ∽
∽![]() ,可得
,可得![]()
∴![]() ∴
∴![]() ,
,
∴![]() ,
,
易证四边形![]() 是矩形,
是矩形,
∴![]() . 又∵
. 又∵![]()
∴![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】2014年全国两会民生话题成为社会焦点.合肥市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了合肥市部分市民,并对调查结果进行整理.绘制了如图所示的不完整的统计图表.
组别 | 焦点话题 | 频数(人数) |
A | 食品安全 | 80 |
B | 教育医疗 | m |
C | 就业养老 | n |
D | 生态环保 | 120 |
E | 其他 | 60 |
请根据图表中提供的信息解答下列问题:
(1)填空:m= ,n= .扇形统计图中E组所占的百分比为 %;
(2)合肥市人口现有750万人,请你估计其中关注D组话题的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注C组话题的概率是多少?