题目内容
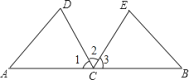
【题目】 [问题解决]:如图1,已知AB∥CD,E是直线AB,CD内部一点,连接BE,DE,若∠ABE=40°,∠CDE=60°,求∠BED的度数.
嘉琪想到了如图2所示的方法,但是没有解答完,下面是嘉淇未完成的解答过程:
解:过点E作EF∥AB,
∴∠ABE=∠BEF=40°
∵AB∥CD,
∴EF∥CD,
…
请你补充完成嘉淇的解答过程:
[问题迁移]:请你参考嘉琪的解题思路,完成下面的问题:
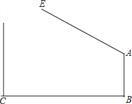
如图3,AB∥CD,射线OM与直线AB,CD分别交于点A,C,射线ON与直线AB,CD分别交于点B,D,点P在射线ON上运动,设∠BAP=α,∠DCP=β.
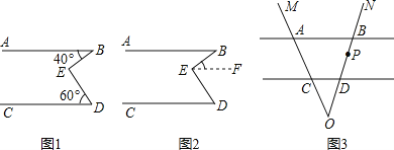
(1)当点P在B,D两点之间运动时(P不与B,D重合),求α,β和∠APC之间满足的数量关系.
(2)当点P在B,D两点外侧运动时(P不与点O重合),直接写出α,β和∠APC之间满足的数量关系.
【答案】[问题解决]见解析;[问题迁移](1) ∠APC=α+β;(2) 当点P在BN上时,∠APC=β-α;当点P在OD上时,∠APC=α-β.
【解析】
问题解决:过点E作EF∥AB,依据平行线的性质,即可得到∠BED的度数;
问题迁移:(1)过P作PQ∥AB,依据平行线的性质,即可得出α,β和∠APC之间满足的数量关系.
(2)分两种情况讨论:过P作PQ∥AB,易得当点P在BN上时,∠APC=β-α;当点P在OD上时,∠APC=α-β.
问题解决:
如图2,过点E作EF∥AB,
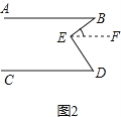
∴∠ABE=∠BEF=40°
∵AB∥CD,
∴EF∥CD,
∴∠B=∠BEF,∠D=∠DEF,
∴∠BED=∠B+∠D=40°+60°=100°;
问题迁移:
(1)如图3,过P作PQ∥AB,
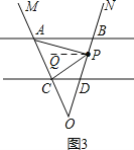
∵AB∥CD,
∴PQ∥CD,
∴∠BAP=∠APQ,∠DCP=∠CPQ,
∴∠APC=∠BAP+∠DCP,即∠APC=α+β;
(2)如图4,当点P在BN上时,∠APC=β-α;
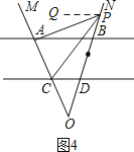
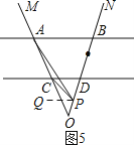
如图5,当点P在OD上时,∠APC=α-β.

【题目】为调动销售人员的积极性,A、B两公司采取如下工资支付方式:A公司每月2000元基本工资,另加销售额的2%作为奖金;B公司每月1600元基本工资,另加销售额的4%作为奖金。已知A、B公司两位销售员小李、小张1~6月份的销售额如下表:
月份 销售额 | 销售额(单位:元) | |||||
1月 | 2月 | 3月 | 4月 | 5月 | 6月 | |
小李(A公司) | 11600 | 12800 | 14000 | 15200 | 16400 | 17600 |
小张(B公司 | 7400 | 9200 | 1100 | 12800 | 14600 | 16400 |
- 请问小李与小张3月份的工资各是多少?
- 小李1~6月份的销售额
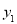 与月份
与月份 的函数关系式是
的函数关系式是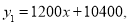 小张1~6月份的销售额
小张1~6月份的销售额 也是月份
也是月份 的一次函数,请求出
的一次函数,请求出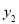 与
与 的函数关系式;
的函数关系式; - 如果7~12月份两人的销售额也分别满足(2)中两个一次函数的关系,问几月份起小张的工资高于小李的工资。