题目内容
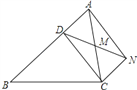
【题目】已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
①求证:AD=CN;
②若∠BAN=90度,求证:四边形ADCN是矩形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:①根据两直线平行,内错角相等求出∠DAC=∠NCA,然后利用“角边角”证明△AMD和△CMN全等,根据全等三角形对应边相等可得AD=CN,然后判定四边形ADCN是平行四边形,再根据平行四边形的对边相等即可得证;
②根据三角形的一个外角等于与它不相邻的两个内角的和推出∠MCD=∠MDC,再根据等角对等边可得MD=MC,然后证明AC=DN,再根据对角线相等的平行四边形是矩形即可得证.
试题解析:①∵CN∥AB,
∴∠DAC=∠NCA,
在△AMD和△CMN中,
∵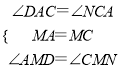 ,
,
∴△AMD≌△CMN(ASA),
∴AD=CN,
又∵AD∥CN,
∴四边形ADCN是平行四边形,
∴CD=AN;
②∵∠AMD=2∠MCD,∠AMD=∠MCD+∠MDC,
∴∠MCD=∠MDC,
∴MD=MC,
由①知四边形ADCN是平行四边形,
∴MD=MN=MA=MC,
∴AC=DN,
∴四边形ADCN是矩形.
考点: 1.矩形的判定;2.全等三角形的判定与性质;3.平行四边形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目