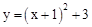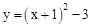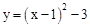题目内容
已知二次函数y=ax2+bx+c的部分图象如图所示,那么下列判断不正确的是( )
| A.ac<0 |
| B.a-b+c>0 |
| C.b=-4a |
| D.关于x的方程ax2+bx+c=0根是x1=-1,x2=5 |
B.
解析试题分析:由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据抛物线与x轴交点及x=1时二次函数的值的情况进行推理,进而对所得结论进行判断:
A、该二次函数开口向下,则a<0;抛物线交y轴于正半轴,则c>0;所以ac<0,正确.
B、由于抛物线过(-1,0),则有:a-b+c =0,错误.
C、由图象知:抛物线的对称轴为 ,即b=-4a,正确.
,即b=-4a,正确.
D、抛物线与x轴的交点为(-1,0)、(5,0);故方程ax2+bx+c=0的根是x1=-1,x2=5,正确.
故选B.
考点:1.二次函数图象与系数的关系;2.抛物线与x轴的交点.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
若二次函数y=x2-2x+k的图象经过点(-1,y1),(3,y2),则y1与y2的大小关系为( )
| A.y1>y2 | B.y1=y2 | C.y1<y2 | D.不能确定 |
二次函数 ,当y<0时,自变量x的取值范围是( )
,当y<0时,自变量x的取值范围是( )
A.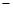 1<x<3 1<x<3 | B.x< 1 1 | C.x>3 | D.x< 1或x>3 1或x>3 |
已知二次函数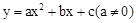 的图象如图所示,有下列5个结论:①
的图象如图所示,有下列5个结论:①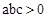 ;②
;②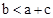 ;③
;③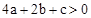 ;④
;④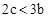 ;⑤
;⑤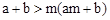 ,(
,(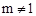 的实数)其中正确的结论有( )
的实数)其中正确的结论有( )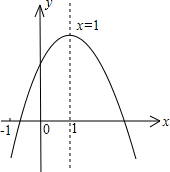
| A.2个 | B.3个 | C.4个 | D.5个 |
若一次函数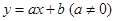 的图象与
的图象与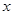 轴的交点坐标为(﹣2,0),则抛物线
轴的交点坐标为(﹣2,0),则抛物线 的对称轴为( )
的对称轴为( )
| A.直线x=1 | B.直线x=﹣2 | C.直线x=﹣1 | D.直线x=﹣4 |
已知二次函数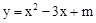 (m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程
(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程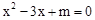 的两实数根是
的两实数根是
| A.x1=1,x2=-1 | B.x1=1,x2=2 |
| C.x1=1,x2=0 | D.x1=1,x2=3 |
二次函数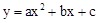 的图象如图所示,反比例函数
的图象如图所示,反比例函数 与一次函数
与一次函数 在同一平面直角坐标系中的大致图象是
在同一平面直角坐标系中的大致图象是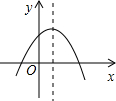
A. | B. | C. | D. |
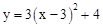

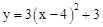
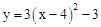
 先向右平移1个单位,再向上平移3个单位,得到新的抛物线解析式是( )
先向右平移1个单位,再向上平移3个单位,得到新的抛物线解析式是( )