题目内容
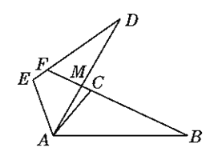
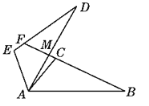
【题目】如图，已知△ABC≌△ADE，BC的延长线交AD于点M，交DE于点F.若∠D＝25°，∠AED＝105°，∠DAC＝10°，求∠DFB的度数．
【答案】60°
【解析】
根据三角形内角和定理可得∠DAE＝50°，再根据全等三角形的性质可得∠B＝∠D＝25°，∠BAC＝∠DAE＝50°，根据角的和差关系可得∠BAD＝60°，再根据三角形外角的性质可得∠AMF的度数，最后根据∠DFB＝∠AMF－∠D即可求解∠DFB的度数．
解：∵∠D＝25°，∠AED＝105°，
∴∠DAE＝50°
又∵△ABC≌△ADE，
∴∠B＝∠D＝25°，∠BAC＝∠DAE＝50°
∵∠DAC＝10°，
∴∠BAD＝60°，
∵∠AMF＝∠BAD＋∠B＝60°＋25°＝85°，
∴∠DFB＝∠AMF－∠D＝85°－25°＝60°
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
【题目】某中学九（2）班同学为了了解2019年某小区家庭月均用水情况，随机调查了该小区的部分家庭，并将调查数据进行如下整理：
月均用水量 | 频数 | 频率 |
| 6 | 0.12 |
| ________ | 0.24 |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | ________ |
| 2 | 0.04 |
请解答以下问题：
（1）把上面的频数分布表和频数分布直方图补充完整；
（2）月均用水量的中位数落在第________小组；
（3）若该小区有1000户家庭，根据调查数据估计，该小区月均用水量超过20吨的家庭大约有多少户？
