��Ŀ����
��֪һ�����߾���O��0��0����B��1��1�����㣬�ҽ���ʽ�Ķ�����ϵ��Ϊ- ��a��0����
��a��0����
����a=1ʱ����������ߵĽ���ʽ�������䷽������������ߵĶ������ꣻ
������֪��A��0��1������������������AB�ཻ�ڵ�M����x���ཻ�ڵ�N������ԭ�㣩����a��ʲô��Χ��ȡֵʱ��ON+BM��ֵΪ��������a��ʲô��Χ��ȡֵʱ��ON-BM��ֵΪ������
��������P��t��t�����������ϣ���Ƶ�PΪ�����ߵIJ����㣮�����������߽���ƽ�ƣ�ʹ��ֻ��һ�������㣬��ʱ�����ߵĶ����Ƿ���ֱ��y=x- �ϣ���˵�����ɣ�
�ϣ���˵�����ɣ�
�⣺��������ߵĽ���ʽΪ ��
��
�������߾�����0��0������1��1�����㣬
�� ��
��
��� ��
��
��������ߵĽ���ʽΪ
����a=1ʱ���������ߵĽ���ʽΪy=-x2+2x��
y=-x2+2x=-��x2-2x+1��+1=-��x-1��2+1��
�������ߵĶ�������Ϊ��1��1����
���ߵ�N��x���ϣ����N��������Ϊ0��
��y=0ʱ���� ��
��
���x1=0��x2=a+1��
�ߵ�N����ԭ�㣬���N������Ϊ��a+1��0����
��ON=a+1��
�ߵ�M������AB�ϣ����M��������Ϊ1��
��y=1ʱ���� ��
��
�����ó� ��
��
���x1=1��x2=a��
��M��������1��1����a��1����
����M������Ϊ��1��1��ʱ��M��B�غϣ�
��ʱa=1��BM=0��ON=2��ON+BM��ON-BM��ֵ���dz���2��
����M������Ϊ��a��1��ʱ��
����M�ڵ�B�Ҳ࣬��ʱa��1��BM=a-1��
��ON+BM=��a+1��+��a-1��=2a��ON-BM=��a+1��-��a-1��=2��
����M�ڵ�B��࣬��ʱ0��a��1��BM=1-a��
��ON+BM=��a+1��+��1-a��=2��ON-BM=��a+1��-��1-a��=2a��
�൱0��a��1ʱ��ON+BM��ֵ�dz���2��
��a��1ʱ��ON-BM��ֵ�dz���2��
������ƽ�ƺ�������ߵĽ���ʽΪ ��
��
�ɲ�����Ķ��壬�÷��̣� ��
��
��t2+��a-2h��t+h2-ak=0��
��ƽ�ƺ��������ֻ��һ�������㣬��˷�����������ȵ�ʵ������
���б�ʽ��=��a-2h��2-4��h2-ak��=0��
��a-4h+4k=0���� ��
��
�ඥ�㣨h��k����ֱ��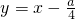 �ϣ�
�ϣ�
�����������������������߾���O��0��0����B��1��1�����㣬�ҽ���ʽ�Ķ�����ϵ��Ϊ- ��������߽���ʽ��������a=1��������ߵĶ������꼴�ɣ�
��������߽���ʽ��������a=1��������ߵĶ������꼴�ɣ�
�������õ�y=0ʱ���� �����x��ֵ�������ó���N�����꣬����������M�ڵ�B�Ҳ࣬��ʱa��1��BM=a-1������M�ڵ�B��࣬��ʱ0��a��1��BM=1-a�ó��𰸼��ɣ�
�����x��ֵ�������ó���N�����꣬����������M�ڵ�B�Ҳ࣬��ʱa��1��BM=a-1������M�ڵ�B��࣬��ʱ0��a��1��BM=1-a�ó��𰸼��ɣ�
��������ƽ�ƺ��������ֻ��һ�������㣬�ʴ˷�����������ȵ�ʵ�������ó��б�ʽ��=��a-2h��2-4��h2-ak��=0���������k��h��a�Ĺ�ϵ���ɵó����㣨h��k����ֱ��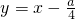 �ϣ�
�ϣ�
������������Ҫ�����˶��κ������ۺ�Ӧ���Լ������б�ʽ�����ʵ�֪ʶ�����÷������۵�˼��ó�M��B�IJ�ͬλ�ù�ϵ�ó����ǽ���ؼ���
 ��
���������߾�����0��0������1��1�����㣬
��
 ��
�����
 ��
����������ߵĽ���ʽΪ

����a=1ʱ���������ߵĽ���ʽΪy=-x2+2x��
y=-x2+2x=-��x2-2x+1��+1=-��x-1��2+1��
�������ߵĶ�������Ϊ��1��1����
���ߵ�N��x���ϣ����N��������Ϊ0��
��y=0ʱ����
 ��
�����x1=0��x2=a+1��
�ߵ�N����ԭ�㣬���N������Ϊ��a+1��0����
��ON=a+1��
�ߵ�M������AB�ϣ����M��������Ϊ1��
��y=1ʱ����
 ��
�������ó�
 ��
�����x1=1��x2=a��
��M��������1��1����a��1����
����M������Ϊ��1��1��ʱ��M��B�غϣ�
��ʱa=1��BM=0��ON=2��ON+BM��ON-BM��ֵ���dz���2��
����M������Ϊ��a��1��ʱ��
����M�ڵ�B�Ҳ࣬��ʱa��1��BM=a-1��
��ON+BM=��a+1��+��a-1��=2a��ON-BM=��a+1��-��a-1��=2��
����M�ڵ�B��࣬��ʱ0��a��1��BM=1-a��
��ON+BM=��a+1��+��1-a��=2��ON-BM=��a+1��-��1-a��=2a��
�൱0��a��1ʱ��ON+BM��ֵ�dz���2��
��a��1ʱ��ON-BM��ֵ�dz���2��
������ƽ�ƺ�������ߵĽ���ʽΪ
 ��
���ɲ�����Ķ��壬�÷��̣�
 ��
����t2+��a-2h��t+h2-ak=0��
��ƽ�ƺ��������ֻ��һ�������㣬��˷�����������ȵ�ʵ������
���б�ʽ��=��a-2h��2-4��h2-ak��=0��
��a-4h+4k=0����
 ��
���ඥ�㣨h��k����ֱ��
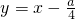 �ϣ�
�ϣ������������������������߾���O��0��0����B��1��1�����㣬�ҽ���ʽ�Ķ�����ϵ��Ϊ-
 ��������߽���ʽ��������a=1��������ߵĶ������꼴�ɣ�
��������߽���ʽ��������a=1��������ߵĶ������꼴�ɣ��������õ�y=0ʱ����
 �����x��ֵ�������ó���N�����꣬����������M�ڵ�B�Ҳ࣬��ʱa��1��BM=a-1������M�ڵ�B��࣬��ʱ0��a��1��BM=1-a�ó��𰸼��ɣ�
�����x��ֵ�������ó���N�����꣬����������M�ڵ�B�Ҳ࣬��ʱa��1��BM=a-1������M�ڵ�B��࣬��ʱ0��a��1��BM=1-a�ó��𰸼��ɣ���������ƽ�ƺ��������ֻ��һ�������㣬�ʴ˷�����������ȵ�ʵ�������ó��б�ʽ��=��a-2h��2-4��h2-ak��=0���������k��h��a�Ĺ�ϵ���ɵó����㣨h��k����ֱ��
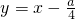 �ϣ�
�ϣ�������������Ҫ�����˶��κ������ۺ�Ӧ���Լ������б�ʽ�����ʵ�֪ʶ�����÷������۵�˼��ó�M��B�IJ�ͬλ�ù�ϵ�ó����ǽ���ؼ���

��ϰ��ϵ�д�
 �óɼ�1��1��ĩ���100��ϵ�д�
�óɼ�1��1��ĩ���100��ϵ�д� ��״Ԫ���źþ�ϵ�д�
��״Ԫ���źþ�ϵ�д�
�����Ŀ
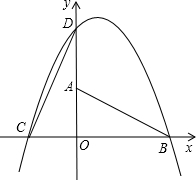 ��OB=4���ֽ�Rt��AOB����ֱ�Ƕ���O����ʱ�뷽����ת90��õ���COD����֪һ�����߾���C��D��B���㣮
��OB=4���ֽ�Rt��AOB����ֱ�Ƕ���O����ʱ�뷽����ת90��õ���COD����֪һ�����߾���C��D��B���㣮 ��a��0����
��a��0���� �ϣ���˵�����ɣ�
�ϣ���˵�����ɣ� ��a��0����
��a��0���� �ϣ���˵�����ɣ�
�ϣ���˵�����ɣ�