Question

【题目】已知：如图1，四边形ABCD四条边上的中点分别为E、F、G、H，顺次连接EF、FG、GH、HE，得到四边形EFGH（即四边形ABCD的中点四边形）．

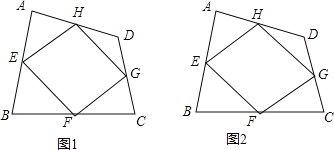
（1）四边形EFGH的形状是 ，证明你的结论．

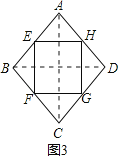
（2）如图2，请连接四边形ABCD的对角线AC与BD，当AC与BD满足 条件时，四边形EFGH是矩形；证明你的结论．

（3）你学过的哪种特殊四边形的中点四边形是矩形？说明理由．

Answer 1

【答案】（1）四边形EFGH是平行四边形；（2）见解析；（3）平行四边形；互相垂直．

【解析】

试题分析：（1）连接BD，根据三角形的中位线定理得到EH∥BD，EH=BD，FG∥BD，FG=BD，推出，EH∥FG，EH=FG，根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形；

（2）根据有一个角是直角的平行四边形是矩形，可知当四边形ABCD的对角线满足AC⊥BD的条件时，四边形EFGH是矩形；

（3）菱形的中点四边形是矩形．根据三角形的中位线平行于第三边并且等于第三边的一半可得EH∥BD，EF∥AC，再根据矩形的每一个角都是直角可得∠1=90°，然后根据平行线的性质求出∠3=90°，再根据垂直定义解答．

解：（1）四边形EFGH的形状是平行四边形．理由如下：

如图1，连结BD．

∵E、H分别是AB、AD中点，

∴EH∥BD，EH=BD，

同理FG∥BD，FG=BD，

∴EH∥FG，EH=FG，

∴四边形EFGH是平行四边形；

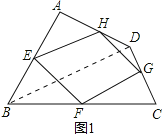
（2）当四边形ABCD的对角线满足互相垂直的条件时，四边形EFGH是矩形．理由如下：

如图2，连结AC、BD．

∵E、F、G、H分别为四边形ABCD四条边上的中点，

∴EH∥BD，HG∥AC，

∵AC⊥BD，

∴EH⊥HG，

又∵四边形EFGH是平行四边形，

∴平行四边形EFGH是矩形；

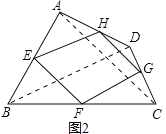
（3）菱形的中点四边形是矩形．理由如下：

如图3，连结AC、BD．

∵E、F、G、H分别为四边形ABCD四条边上的中点，

∴EH∥BD，HG∥AC，FG∥BD，EH=BD，FG=BD，

∴EH∥FG，EH=FG，

∴四边形EFGH是平行四边形．

∵四边形ABCD是菱形，

∴AC⊥BD，

∵EH∥BD，HG∥AC，

∴EH⊥HG，

∴平行四边形EFGH是矩形．

故答案为：平行四边形；互相垂直．