题目内容
【题目】某社区计划对面积为1200m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.
(1)甲、乙两施工队每天分别能完成绿化的面积是多少?
(2)设先由甲队施工x天,再由乙队施工y天,刚好完成绿化任务,求y与x的函数解析式;
(3)在(2)的情况下,若甲队绿化费用为1600元/天,乙队绿化费用为700元/天,在施工过程中每天需要支付高温补贴a元(100≤a≤300),且工期不得超过14天,则如何安排甲,乙两队施工的天数,使施工费用最少?
【答案】(1)甲、乙两施工队每天分别能完成绿化的面积是100 m2、50 m2;
(2)y=24-2x;
(3)当100≤a≤200时,甲队施工10天,乙队施工4天费用最小,为18800+14a,
当200≤a≤300时,甲队施工11天,乙队施工2天费用最小,为19000+12a
【解析】
(1)设乙施工队每天能完成绿化的面积是xm2,则甲施工队每天能完成绿化的面积是2xm2,根据题意列出分式方程即可求解;
(2)根据总社区计划对面积为1200m2,即可列出函数关系式;
(3)先根据工期不得超过14天,求出x的取值,再根据列出总费用w的函数关系式,即可求解.
(1)设乙施工队每天能完成绿化的面积是xm2,则甲施工队每天能完成绿化的面积是2xm2,根据题意![]() ,解得x=50,
,解得x=50,
经检验,x=50是方程的解,
故甲、乙两施工队每天分别能完成绿化的面积是100 m2、50 m2;
(2)依题意得100x+50y=1200,
化简得y=24-2x,
故求y与x的函数解析式为y=24-2x;
(3)∵工期不得超过14天,
∴x+y≤14,0≤x≤14,0≤y≤14
即x+24-2x≤14,解得x≥10,
∴x的取值为10≤x≤12;
设总施工费用为w,则当x=10时,w=(1600+a)×10+(700+a)×4=18800+14a,
当x=11时,w=(1600+a)×11+(700+a)×2=19000+12a
当x=12时,w=(1600+a)×12=19200+12a,
∵100≤a≤300,经过计算得
当100≤a≤200时,甲队施工10天,乙队施工4天费用最小,为18800+14a,
当200≤a≤300时,甲队施工11天,乙队施工2天费用最小,为19000+12a

 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案【题目】为了进一步了解某校八年级学生的身体素质情况,体育老师对该校八年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
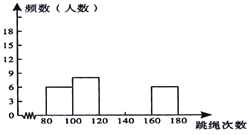
请结合图表完成下列问题:
(1)求表中a的值并把频数分布直方图补充完整;
(2)该班学生跳绳的中位数落在第 组,众数落在第 组;
(3)若在一分钟内跳绳次数少于120次的为测试不合格,则该校八年级共1000人中,一分钟跳绳不合格的人数大约有多少?