题目内容
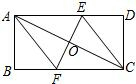 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E,交BC边于F,分别连接AF和CE,AE=10.在线段AC上是否存在一点P,使得2AE2=AC•AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E,交BC边于F,分别连接AF和CE,AE=10.在线段AC上是否存在一点P,使得2AE2=AC•AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.
分析:过E作EP⊥AD交AC于P,则P就是所求的点,首先证明四边形AFCE是菱形,然后根据题干条件证明△AOE∽△AEP,列出关系式.
解答: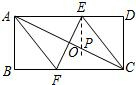 证明:过E作EP⊥AD交AC于P,则P就是所求的点.
证明:过E作EP⊥AD交AC于P,则P就是所求的点.
当顶点A与C重合时,折痕EF垂直平分AC,
∴OA=OC,∠AOE=∠COF=90°,
∵在平行四边形ABCD中,AD∥BC,
∴∠EAO=∠FCO,
∴△AOE≌△COF,
∴OE=OF
∴四边形AFCE是菱形.
∴∠AOE=90°,又∠EAO=∠EAP,
由作法得∠AEP=90°,
∴△AOE∽△AEP,
∴
=
,则AE2=A0•AP,
∵四边形AFCE是菱形,
∴AO=
AC,
∴AE2=
AC•AP,
∴2AE2=AC•AP.
 证明:过E作EP⊥AD交AC于P,则P就是所求的点.
证明:过E作EP⊥AD交AC于P,则P就是所求的点.当顶点A与C重合时,折痕EF垂直平分AC,
∴OA=OC,∠AOE=∠COF=90°,
∵在平行四边形ABCD中,AD∥BC,
∴∠EAO=∠FCO,
∴△AOE≌△COF,
∴OE=OF
∴四边形AFCE是菱形.
∴∠AOE=90°,又∠EAO=∠EAP,
由作法得∠AEP=90°,
∴△AOE∽△AEP,
∴
| AE |
| AP |
| AO |
| AE |
∵四边形AFCE是菱形,
∴AO=
| 1 |
| 2 |
∴AE2=
| 1 |
| 2 |
∴2AE2=AC•AP.
点评:本题主要考查翻折变换的折叠问题,还涉及到的知识点有全等三角形的判定与性质.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
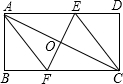 痕EF交AD边于E,交BC边于F,分别连接AF、CE和EF,设EF与AC的交点为O.
痕EF交AD边于E,交BC边于F,分别连接AF、CE和EF,设EF与AC的交点为O. (2013•乐清市模拟)已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连接AF和CE.
(2013•乐清市模拟)已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连接AF和CE. 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.求证:四边形AFCE是菱形.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.求证:四边形AFCE是菱形.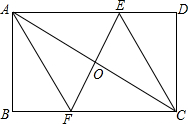 已知:如图所示的一张矩形纸片ABCD(AD>AB),O是对角线AC的中点,过点O的直线EF⊥AC交AD边于E,交BC边于F.
已知:如图所示的一张矩形纸片ABCD(AD>AB),O是对角线AC的中点,过点O的直线EF⊥AC交AD边于E,交BC边于F.