题目内容
已知：如图所示的一张矩形纸片ABCD（AD＞AB），将纸片折叠一次，使点A与点C重合，再展开，折痕EF交AD边于点E，交BC边于点F，分别连结AF和CE．求证：四边形AFCE是菱形．分析：由四边形ABCD是矩形，根据矩形与折叠的性质，即可证得△AEO≌△CFO，继而证得AE=CE=CF=AF，继而可证得：四边形AFCE是菱形．
解答：证明：∵四边形ABCD是矩形，
∴AD∥BC，
∴∠EAO=∠FCO，
由折叠的性质可得：OA=OC，AE=CE，AF=CF，
在△OAE和△OCF中，
，
∴△AEO≌△CFO（AAS），
∴AE=CF，
∴AE=CE=CF=AF，
∴四边形AFCE是菱形．
∴AD∥BC，
∴∠EAO=∠FCO，
由折叠的性质可得：OA=OC，AE=CE，AF=CF，
在△OAE和△OCF中，
|
∴△AEO≌△CFO（AAS），
∴AE=CF，
∴AE=CE=CF=AF，
∴四边形AFCE是菱形．
点评：此题考查了菱形的判定，矩形的性质以及全等三角形的判定与性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
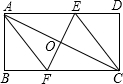痕EF交AD边于E，交BC边于F，分别连接AF、CE和EF，设EF与AC的交点为O．
（2013•乐清市模拟）已知：如图所示的一张矩形纸片ABCD（AD＞AB），将纸片折叠一次，使点A与点C重合，再展开，折痕EF交AD边于点E，交BC边于点F，分别连接AF和CE．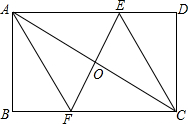
已知：如图所示的一张矩形纸片ABCD（AD＞AB），O是对角线AC的中点，过点O的直线EF⊥AC交AD边于E，交BC边于F．