题目内容
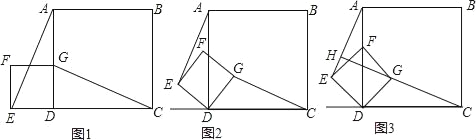
【题目】(1)如图1,正方形ABCD和正方形DEFG,G在AD边上,E在CD的延长线上.求证:AE=CG,AE⊥CG;
(2)如图2,若将图1中的正方形DEFG绕点D顺时针旋转角度θ(0°<θ<90°),此时AE=CG还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3)如图3,当正方形DEFG绕点D顺时针旋转45°时,延长CG交AE于点H,当AD=4,DG=![]() 时,求线段CH的长.
时,求线段CH的长.
【答案】(1)(2)见解析;(3)![]() .
.
【解析】试题分析:(1)先判断出△ADE≌△CDG,然后用互余判断出垂直;
(2)先判断出△ADE≌△CDG,然后用互余判断出垂直;
(3)先判断出△ADE≌△CDG,然后用互余判断出垂直,然后用勾股定理计算出CM,AM最后用相似即可.
试题解析:(1)在△ADE和△CDG中,
DE=DG,∠ADE=∠CDG,AD=CD,
∴△ADE≌△CDG,
∴AE=CG,∠AED=∠CGD,
∵∠DCG+∠CGD=90°,
∴∠DCG+∠AED=90°,
∴AE⊥CG.
(2)∵∠CDG+∠ADG=90°,∠ADE+∠ADG=90°,
∴∠CDG=∠ADE
在△ADE和△CDG中,
DE=DG,∠ADE=∠CDG,AD=CD,
∴△ADE≌△CDG,
∴AE=CG,∠AED=∠CGD,
∵∠DCG+∠CGD=90°,
∴∠DCG+∠AED=90°,
∴AE⊥CG.
(3)如图,
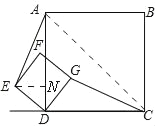
过点E作AD的垂线,垂足为N,连接AC,
在△ADE和△CDG中,
DE=DG,∠ADE=∠CDG,AD=CD,
∴△ADE≌△CDG,
∴∠EAD=∠DCM
∴tan∠DCM=![]() ,
,
∴DM=![]() CD=
CD=![]()
∴CM=![]() =
=![]() ,AM=AD﹣DM=
,AM=AD﹣DM=![]()
∵△CMD∽△AMH,
∴![]() ,
,
∴AH=![]() ,
,
∴CH=![]() =
=![]() .
.

练习册系列答案
相关题目