题目内容
 21、完成下列证明过程:
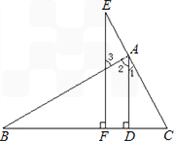
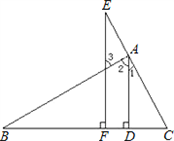
21、完成下列证明过程:已知:如图,AD⊥BC于D,EF⊥BC于F,∠1=∠3,
求证:AD平分∠BAC.
证明:∵AD⊥BC于D
EF⊥BC于F(已知)
∴∠ADB=∠EFB=90°()
∴AD∥EF()
∴∠1=∠E()
∠2=∠3()
又∵∠3=∠1(已知)
∴∠1=∠2()
∴AD平分∠BAC.
分析:因为∠ADB=∠EFB,由同位角相等证明AD∥EF,则有∠1=∠E,∠2=∠3,又因为∠3=∠1,所以有∠1=∠2,故AD平分∠BAC.
解答:证明:∵AD⊥BC于D,
EF⊥BC于F,
∴∠ADB=∠EFB=90°(垂线的性质)
∴AD∥EF(同位角相等,两直线平行)
∴∠1=∠E(两直线平行,同位角相等)
∠2=∠3(同位角相等,内错角相等)
又∵∠3=∠1(已知)
∴∠1=∠2(等量代换)
∴AD平分∠BAC(角平分线定义).
EF⊥BC于F,
∴∠ADB=∠EFB=90°(垂线的性质)
∴AD∥EF(同位角相等,两直线平行)
∴∠1=∠E(两直线平行,同位角相等)
∠2=∠3(同位角相等,内错角相等)
又∵∠3=∠1(已知)
∴∠1=∠2(等量代换)
∴AD平分∠BAC(角平分线定义).
点评:此题是一道把平行线的性质和判定、角平分线的定义结合求解的综合题.有利于培养学生综合运用数学知识的能力.

练习册系列答案
相关题目


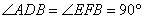 ( )
( )