Question

【题目】如图（1），在平面直角坐标系中，已知点A（m，0），B（n，0），且m，n满足（m+1）2+＝0，将线段AB向右平移1个单位长度，再向上平移2个单位长度，得到线段CD，其中点C与点A对应，点D与点B对应，连接AC，BD．

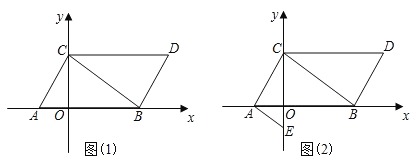
（1）求点A、B、C、D的坐标；

（2）在x轴上是否存在点P，使三角形PBC的面积等于平行四边形ABDC的面积？若存在，求出点P的坐标；若不存在，请说明理由；

（3）如图（2），点E在y轴的负半轴上，且∠BAE＝∠DCB．求证：AE∥BC．

Answer 1

【答案】（1）A（﹣1，0），B（3，0），C（0，2），D（4，2）；（2）存在，点P的坐标为（11，0）或（﹣5，0）；（3）见解析．

【解析】

（1）由非负数的性质得出，且，求出，，得出，，由平移的性质得，；

（2）设，由（1）得，，则，由得出，解得，或，即可得出答案；

（3）由平移的性质得，由平行线的性质得出，证出，即可得出结论．

（1）解：∵m，n满足（m+1）2+＝0，

∴m+1＝0，且n﹣3＝0，

∴m＝﹣1，n＝3，

∴A（﹣1，0），B（3，0），

由平移的性质得：C（0，2），D（4，2）；

（2）解：存在，理由如下：

设P（x，0），

由（1）得：AB＝4，OC＝2，

∴S平行四边形ABDC＝4×2＝8，

∵PB＝|x﹣3|，

∴S△PBC＝PB×OC＝|x﹣3|×2＝8，

解得：x＝11，或x＝﹣5，

∴点P的坐标为（11，0）或（﹣5，0）；

（3）证明：由平移的性质得：AB∥CD，

∴∠DCB＝∠CBA，

∵∠BAE＝∠DCB，

∴∠BAE＝∠CBA，

∴AE∥BC．