题目内容
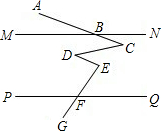如图，直线MN∥PQ，∠ABM=30°，∠D=40°，∠EFQ=70°，则∠C+∠E=________．
140°
分析：分别过点C、D、E作直线CK∥MN，DT∥CK，EL∥DT，故可得出CK∥MN∥DT∥EL∥PQ，再由平行线的性质即可得出结论．
解答：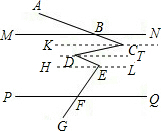
解：分别过点C、D、E作直线CK∥MN，DT∥CK，EL∥DT，
∵MN∥PQ，
∴CK∥MN∥DT∥EL∥PQ，
∵∠ABM=30°，
∴∠BCK=∠ABM=30°，∠KCD=∠CDT，∠DEH=∠TDE，∠HEF=∠EFQ=70°，
∴∠C+∠E=∠BCK+∠KCD+∠DEH+∠HEF=∠ABM+∠C+∠EFQ=30°+40°+70°=140°．
故答案为：140°．
点评：本题考查的是平行线的性质，根据题意作出辅助线，构造出平行线是解答此题的关键．
分析：分别过点C、D、E作直线CK∥MN，DT∥CK，EL∥DT，故可得出CK∥MN∥DT∥EL∥PQ，再由平行线的性质即可得出结论．
解答：
解：分别过点C、D、E作直线CK∥MN，DT∥CK，EL∥DT，∵MN∥PQ，
∴CK∥MN∥DT∥EL∥PQ，
∵∠ABM=30°，
∴∠BCK=∠ABM=30°，∠KCD=∠CDT，∠DEH=∠TDE，∠HEF=∠EFQ=70°，
∴∠C+∠E=∠BCK+∠KCD+∠DEH+∠HEF=∠ABM+∠C+∠EFQ=30°+40°+70°=140°．
故答案为：140°．
点评：本题考查的是平行线的性质，根据题意作出辅助线，构造出平行线是解答此题的关键．
练习册系列答案
相关题目
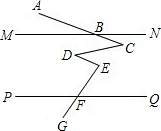（2009•荆州二模）如图，直线MN∥PQ，∠ABM=30°，∠D=40°，∠EFQ=70°，则∠C+∠E=
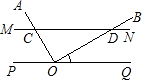如图，直线MN∥PQ．点O在PQ上．射线OA⊥OB，分别交MN于点C和点D．∠BOQ=30°．若将射线OB绕点O逆时针旋转30°，则图中60°的角共有（ ）
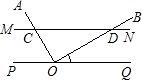如图，直线MN∥PQ．点O在PQ上．射线OA⊥OB，分别交MN于点C和点D．∠BOQ=30°．若将射线OB绕点O逆时针旋转30°，则图中60°的角共有