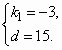��Ŀ����
��֪һԪ���η���x2��4x��5��0������ʵ����Ϊx1��x2����x1��x2����x1��x2�ֱ���������y����x2��bx��c��x�����������A��B�ĺ�����(����ͼ��ʾ)��
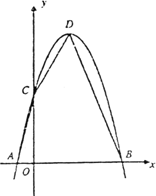
(1)��������ߵĽ���ʽ��
(2)��(1)�е���������y��Ľ���ΪC�������ߵĶ���ΪD����ֱ��д����C��D�����겢����ı���ABDC�������
(3)�Ƿ����ֱ��y��kx(k��0)���߶�BD�ཻ�Ұ��ı���ABDC�������Ϊ��ȵ������֣������ڣ����k��ֵ���������ڣ���˵�����ɣ�
[ע��������y��ax2��bx��c(a��0)�Ķ�������Ϊ(![]() )]
)]
������
|
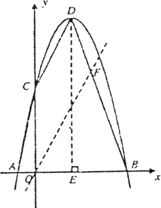
�����⣺(1)�ɷ���x2��4x��5��0�÷��̵�����x1����1��x2��5�� ��������A��B������ֱ�ΪA(��1��0)��B(5��0)������1�� ������A(��1��0)��B(5��0)����y����x2��bx��c�� ���� �����������ߵĽ���ʽΪy����x2��4x��5����������������������3�� ����(2)C(0��5)��D(2��9)��������������������������������5�� ������ͼ��ʾ����D��DE��x���ڵ�E����
����S�ı���ACDB��S��AOC��S�ı���OCDE��S��EDB ������ ������ ������16��14 ������30��������������������������������������7�� ����(3)��������������ֱ�ߣ�������������������8�� �������B��D�����ֱ�߽���ʽΪy��k1x��d����B(5��0)��D(2��9)����y��k1x��d�� ���� ������� ������ֱ��BD�Ľ���ʽΪy����3x��15����������������������10�� ������y��kx��y����3x��15�Ľ���ΪF(m��n)����ֱ��OF����S��OBF�� ������ �����֡ߵ�F(m��6)��y����3x��15�ϣ� ������6����3m��15�� ������m��3�� �������F(3��6)����������������������������������������11�� �����ѵ�F(3��6)����y��kx����6��3k����k��2����������������12�� |

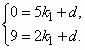 ������������������������9��
������������������������9��