题目内容
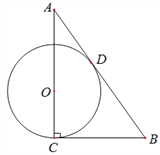
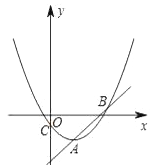
【题目】如图,在正方形![]() 中,
中,![]() 在
在![]() 边上,
边上,![]() 在
在![]() 边上,且
边上,且![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )
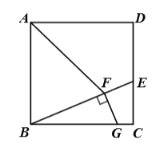
A. 10B. 11C. 12D. 13
【答案】D
【解析】
过点A作AH⊥BE于K,交BC于H,设AB=m,由正方形性质和等腰三角形性质可证明:△BKH∽△BFG,BH=![]() BG,再证明△ABH≌△BCE,可得BH=CE,可列方程
BG,再证明△ABH≌△BCE,可得BH=CE,可列方程![]() (m2)=m7,即可求得BC=12,CE=5,由勾股定理可求得BE.
(m2)=m7,即可求得BC=12,CE=5,由勾股定理可求得BE.
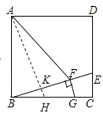
解:如图,过点A作AH⊥BE于K,交BC于H,设AB=m,
∵正方形ABCD
∴BC=CD=AB=m,∠ABH=∠C=90°
∵CG=2,DE=7,
∴CE=m7,BG=m2
∵FG⊥BE
∴∠BFG=90°
∵AF=AB,AH⊥BE
∴BK=FK,即BF=2BK,∠BKH=90°=∠BFG
∴△BKH∽△BFG
∴![]() ,即BH=
,即BH=![]() BG=
BG=![]() (m2)
(m2)
∵∠ABK+∠CBE=∠ABK+∠BAH=90°
∴∠BAH=∠CBE
在△ABH和△BCE中,∠BAH=∠CBE,AB=BC,∠ABH=∠BCE,
∴△ABH≌△BCE(ASA)
∴BH=CE
∴![]() (m2)=m7,解得:m=12
(m2)=m7,解得:m=12
∴BC=12,CE=127=5
在Rt△BCE中,BE=![]() .
.
故选:D.

练习册系列答案
相关题目