��Ŀ����
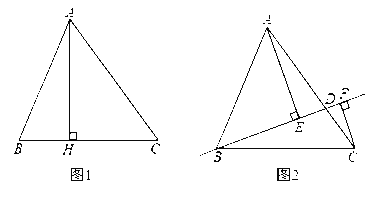
����Ŀ����ͼ1��2���ڡ�ABC�У�AB=13��BC=14��BH=5��
̽������ͼ1��AH��BC�ڵ�H����AH= ��AC= ����ABC�����![]() ��
��
��չ����ͼ2����D��AC�ϣ������A��C�غϣ����ֱ����A.C��ֱ��BD�Ĵ��ߣ�����ΪE��F����BD=x��AE=m��CF=n������D���A�غ�ʱ��������Ϊ![]() ��
��
��1���ú�x��m��n�Ĵ���ʽ��ʾ![]() ��
��![]() ��
��
��2����m+n����x�ĺ�����ϵʽ������m+n�������ֵ����Сֵ��
��3���Ը�����һ��xֵ����ʱֻ��ȷ��Ψһ�ĵ�D��ֱ��д��������x��ȡֵ��Χ��
���𰸡�̽����12��15��84����չ��(1)![]() =
=![]() mx��
mx��![]() =
=![]() nx��(2)m+n=
nx��(2)m+n=![]() ��m+n�����ֵ15��m+n����СֵΪ12��(3) 11.2.
��m+n�����ֵ15��m+n����СֵΪ12��(3) 11.2.
�����������������̽�������ݹ��ɶ������㼴�ɣ�
��չ����1�����������ε������ʽ���㣻
��2��������ABC�������84���г���ϵʽ�������m+n����x�ĺ�����ϵʽ�����ͼ�������m+n�������ֵ����Сֵ��
��3�����ݵ�BD��ACʱ��m+n�����ֵ���
���������̽�����ɹ��ɶ����ã�AH=![]() =12��
=12��
AC=![]() =15��
=15��
��ABC�����S��ABC=![]() ��BC��AH=84.
��BC��AH=84.
�ʴ�Ϊ��12��15��84��
��չ����1��![]() =
=![]() ��BD��AE=
��BD��AE=![]() mx��
mx��
![]() =
=![]() ��BD��CH=
��BD��CH=![]() nx��
nx��
��2��![]() mx+
mx+![]() nx=84��
nx=84��
m+n=![]() ��
��
��BD��ACʱ��m+n�����ֵ15��
��BDֵ���ʱ��m+n����Сֵ��
������D���C�غ�ʱm+n����Сֵ��
��m+n����СֵΪ![]() =12��
=12��
��3����BD��ACʱ��
x=BD=![]() =11.2��ֻ��ȷ��Ψһ�ĵ�D��
=11.2��ֻ��ȷ��Ψһ�ĵ�D��