Question

【题目】如图，AB∥CD，EF与AB、CD分别相交于点E、F，EP⊥EF，与∠EFD的平分线FP相交于点P，且∠BEP=20°，则∠EPF=（ ）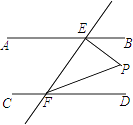

A.70°
B.65°
C.55°
D.45°

Answer 1

【答案】C
【解析】∵EP⊥EF，

∴∠PEF=90°，

∵∠BEP=20°，

∴∠AEF=180°﹣∠PEF﹣∠BEP=180°﹣90°﹣20°=70°，

∵AB∥CD，

∴∠EFD=∠AEF=70°，

∵FP是∠EFD的平分线，

∴∠EFP= ∠EFD= ×70°=35°，

在△EFP中，∠EPF=180°﹣90°﹣35°=55°．

所以答案是：C．

【考点精析】解答此题的关键在于理解垂线的性质的相关知识，掌握垂线的性质：1、过一点有且只有一条直线与己知直线垂直．2、垂线段最短，以及对平行线的性质的理解，了解两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．