题目内容
26、在2004，2005，2006，2007这四个数中，不能表示为两个整数平方差的数是（ ）
分析：由a2-b2=（a-b）（a+b）可知，两个整数平方差可分解为两个整数的积，且两个因数同为奇数或者偶数，由此进行逐一判断．
解答：解：由于a2-b2=（a-b）（a+b）
2007=10042-10032，
2005=10032-10022，
2004=5022-5002，
而2006=2×1003，
a-b与a+b的奇偶性相同，2×1003一奇、一偶，
故2006不能表示为两个整数平方差．
故选B．
2007=10042-10032，
2005=10032-10022，
2004=5022-5002，
而2006=2×1003，
a-b与a+b的奇偶性相同，2×1003一奇、一偶，
故2006不能表示为两个整数平方差．
故选B．
点评：本题考查了平方差公式的实际运用，使学生体会到平方差公式在判断数的性质方面的作用．
练习册系列答案
相关题目
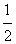与2005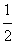
之间有（ ）个整数，它们的和是（ ），积是（ ）。