题目内容
【题目】如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A.点B同时出发,沿三角形的边运动,已知点M的速度为2cm/s,点N的速度为3cm/s.当点N第一次到达B点时,M、N同时停止运动.
(1)点M、N运动 秒后,△AMN是等边三角形?
(2)点M、N在BC边上运动时,运动 秒后得到以MN为底边的等腰三角形△AMN?
(3)M、N同时运动几秒后,△AMN是直角三角形?请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)点M、N运动3秒或
;(3)点M、N运动3秒或![]() 秒或10秒或9秒后,△AMN为直角三角形.
秒或10秒或9秒后,△AMN为直角三角形.
【解析】
(1)当AM=AN时,△MNA是等边三角形.设运动时间为t秒,构建方程即可解决问题;
(2)点M、N在BC边上运动时,满足CM=BN时,可以得到以MN为底边的等腰三角形△AMN.构建方程即可解决问题;
(3)据题意设点M、N运动t秒后,可得到直角三角形△AMN,分四种情况讨论即可.
(1)当AM=AN时,△MNA是等边三角形,设运动时间为t秒
则有:2t=12﹣3t
解得t=![]()
故点M、N运动![]() 秒后,△AMN是等边三角形;
秒后,△AMN是等边三角形;
(2)点M、N在BC边上运动时,满足CM=BN时,可以得到以MN为底边的等腰三角形△AMN
则有:2t﹣12=36﹣3t
解得t=![]()
故运动![]() 秒后得到以MN为底边的等腰三角形△AMN;
秒后得到以MN为底边的等腰三角形△AMN;
(3)设点M、N运动t秒后,可得到直角三角形△AMN
①当M在AC上,N在AB上,∠ANM=90°时,如图
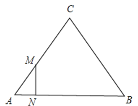
∵∠A=60°
∴∠AMN=30°
∴AM=2AN
则有2t=2(12﹣3t)
∴t=3;
②当M在AC上,N在AB上,∠AMN=90°时,如图

∵∠A=60°
∴∠ANM=30°
∴2AM=AN
∴4t=12﹣3t
∴t=![]() ;
;
③当M、N都在BC上,∠ANM=90°时,如图

CN=3t﹣24=6
解得t=10;
④当M、N都在BC上,∠AMN=90°时,则N与B重合,M正好处于BC的中点,如图

此时2t=12+6
解得t=9;
综上所述,点M、N运动3秒或![]() 秒或10秒或9秒后,△AMN为直角三角形.
秒或10秒或9秒后,△AMN为直角三角形.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案





