��Ŀ����
����Ŀ������ѧ��ȤС���У�С��������ѧ̽��������߳�Ϊ2��������ABCD��߳�Ϊ2![]() ��������AEFG��ͼ1λ�÷��ã�AD��AE��ͬһֱ���ϣ�AB��AG��ͬһֱ������
��������AEFG��ͼ1λ�÷��ã�AD��AE��ͬһֱ���ϣ�AB��AG��ͬһֱ������
��1��С������DG��BE���������˵��������
��2����ͼ2��С����������ABCD�Ƶ�A��ʱ����ת������Bǡ�������߶�DG��ʱ��������������ʱBE�ij���
��3����ͼ3��С����������ABCD�Ƶ�A������ʱ����ת���߶�DG���߶�BE���ཻ������ΪH��д����GHE����BHD���֮�͵����ֵ������Ҫ˵��������

���𰸡���1�����ɼ���������2��![]() ����3��6�����ɼ�������
����3��6�����ɼ�������
��������
�����������1�����ı���ABCD���ı���AEFGΪ�����Σ����������ε����ʵõ����Ա���ȣ��Ҽн���ȣ�����SAS�õ�������ADG��������ABEȫ�ȣ�����ȫ�������ζ�Ӧ����ȵ���AGD=��AEB����ͼ1��ʾ���ӳ�EB��DG�ڵ�H�����õȽǵ������ȵõ���DHE=90�������ô�ֱ�Ķ��弴�ɵ�DG��BE��
��2�����ı���ABCD���ı���AEFGΪ�����Σ����������ε����ʵõ����Ա���ȣ��Ҽн���ȣ�����SAS�õ�������ADG��������ABEȫ�ȣ�����ȫ�������ζ�Ӧ����ȵõ�DG=BE����ͼ2������A��AM��DG��DG�ڵ�M����AMD=��AMG=90������ֱ��������AMD�У����AM�ij�����ΪDM�ij������ݹ��ɶ������GM�ij�������ȷ����DG�ij�����ΪBE�ij���
��3����GHE����BHD���֮�͵����ֵΪ6������Ϊ��������EGH����H����EGΪֱ����Բ�ϣ�������H���A�غ�ʱ����EGH�ĸ��������BDH����H����BDΪֱ����Բ�ϣ�������H���A�غ�ʱ����BDH�ĸ������ȷ������������ֵ��
�����������1�����ı���ABCD���ı���AEFG��Ϊ�����Σ�
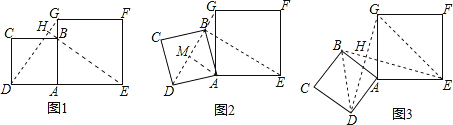
��AD=AB����DAG=��BAE=90����AG=AE��
����ADG����ABE��
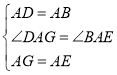 ��
��
���ADG�ա�ABE��SAS����
���AGD=��AEB��
��ͼ1��ʾ���ӳ�EB��DG�ڵ�H��
����ADG����AGD+��ADG=90����
���AEB+��ADG=90����
����EDH����AEB+��ADG+��DHE=180����
���DHE=90����
��DG��BE��
��2�����ı���ABCD���ı���AEFG��Ϊ�����Σ�
��AD=AB����DAB=��GAE=90����AG=AE��
���DAB+��BAG=��GAE+��BAG������DAG=��BAE��
����ADG����ABE��
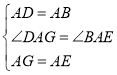
���ADG�ա�ABE��SAS����
��DG=BE��
��ͼ2������A��AM��DG��DG�ڵ�M����AMD=��AMG=90����
��BDΪ������ABCD�ĶԽ��ߣ�
���MDA=45����
��Rt��AMD����MDA=45����
��cos45��=![]() ��
��
��AD=2��
��DM=AM=![]() ��
��
��Rt��AMG�У����ݹ��ɶ����ã�GM=![]() ��
��
��DG=DM+GM=![]() ��
��
��BE=DG=![]() ��
��
��3����GHE����BHD���֮�͵����ֵΪ6������Ϊ��
������EGH����H����EGΪֱ����Բ�ϣ�
������H���A�غ�ʱ����EGH�ĸ����
������BDH����H����BDΪֱ����Բ�ϣ�
������H���A�غ�ʱ����BDH�ĸ����
����GHE����BHD���֮�͵����ֵΪ2+4=6��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�