Question

【题目】探究题：

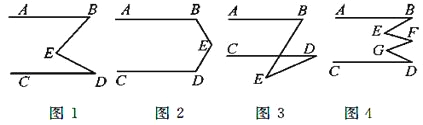
(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗？

(2)若将点E移至图2的位置,此时∠B，∠D，∠E之间有什么关系？

(3)若将点E移至图3的位置,此时∠B，∠D，∠E之间的关系又如何？

(4)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系？

Answer 1

【答案】（1）相等（2）∠B+∠D+∠E=360°（3）∠B=∠D+∠E（4）相等

【解析】试题分析：（1）过点E作EF∥AB，由平行线的性质可知∠B=∠BEF，∠D=∠DEF，再由角之间的关系即可得出结论；

（2）过点E作EF∥AB，由平行线的性质可知∠B+∠BEF=180°，∠D+∠DEF=180°，再由角之间的关系即可得出结论；

（3）过点E作EF∥AB，由平行线的性质可知∠B=∠BEF，∠D=∠DEF，再由角之间的关系即可得出结论；

（4）过点F作FM∥AB，用（1）的结论可知∠E=∠B+∠EFM，∠G=∠GFM+∠D，再由角之间的关系即可得出结论．

试题解析：解：（1）相等，过点E作EF∥AB，如图1所示．

∵EF∥AB，∴∠B=∠BEF．∵EF∥AB∥CD，∴∠D=∠DEF，∴∠BED=∠BEF+∠DEF=∠B+∠D．

（2）过点E作EF∥AB，如图2所示．

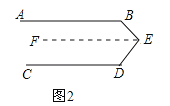
∵AB∥EF，∴∠B+∠BEF=180°．∵EF∥AB∥CD，∴∠D+∠DEF=180°，∴∠B+∠BEF+∠D+∠DEF=180°+180°．∵∠E=∠BEF+∠DEF，∴∠B+∠D+∠E=360°．

（3）过点E作EF∥AB，如图3所示．

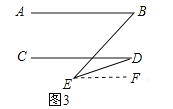
∵AB∥EF，∴∠B=∠BEF．∵EF∥AB∥CD，∴∠D=∠DEF，∴∠E=∠BEF﹣∠DEF=∠B﹣∠D．

（4）过点F作FM∥AB，如图4所示．

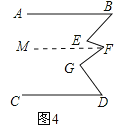
∵AB∥FM，结合（1）结论，∴∠E=∠B+∠EFM．∵FM∥AB∥CD，结合（1）结论，∴∠G=∠GFM+∠D．又∵∠F=∠EFM+∠GFM，∴∠E+∠G=∠B+∠D+∠F．