题目内容
【题目】如图,已知AB∥CD,∠B=∠C,求证:∠1=∠2.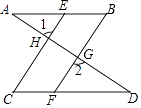
证明:∵AB∥CD(已知)
∴∠B=().
∵∠B=∠C(已知)
∴∠BFD=∠C()
∴∥()
∴∠2=(两直线平行,同位角相等)
∵∠1=()
∴∠1=∠2(等量代换).
【答案】∠BFD;两直线平行,内错角相等;等量代换;BC;BF;同位角相等,两直线平行;∠CHG;∠CHG;对顶角相等
【解析】证明:∵AB∥CD(已知)
∴∠B=∠BFD(两直线平行,内错角相等).
∵∠B=∠C(已知)
∴∠BFD=∠C(等量代换)
∴BC∥BF(同位角相等,两直线平行)
∴∠2=∠CHG(两直线平行,同位角相等)
∵∠1=∠CHG(对顶角相等)
∴∠1=∠2(等量代换).
故答案是:∠BFD; 两直线平行,内错角相等; 等量代换;BC;BF;∠CHG;∠CHG; 对顶角相等.
【考点精析】掌握平行线的判定与性质是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.

 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案【题目】把文字翻译成数学符号,构建方程组模型是解此类题的关键某超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表统计了近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800 |
第二周 | 6台 | 8台 | 3180 |
(1)求A、B两种型号的电风扇每台的销售价分别是多少元?
(2)若超市准备用不超过5250元的金额再采购这两种型号的电风扇共30台,
①求A种型号的电风扇最多能采购多少台?
②超市销售完这30台电风扇是否能实现利润不低于1240元的目标?若能实现,请写出相应的采购方案,若不能实现,请说明理由.
(进价、售价均保持不变,利润=销售收入﹣进货成本)