题目内容
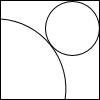 如图所示:在一边长为46cm的正方形纸片上剪下一块圆形和一个扇形纸片,使之恰好做成一个圆锥形模型,它的底面半径是
如图所示:在一边长为46cm的正方形纸片上剪下一块圆形和一个扇形纸片,使之恰好做成一个圆锥形模型,它的底面半径是分析:设小圆的半径为r,可求得小圆的周长,利用扇形的弧长公式可得大扇形的半径,根据大扇形的半径+小扇形的半径+小扇形的半径的
倍=正方形的对角线长可得小扇形的半径,也就是圆锥的底面半径.
| 2 |
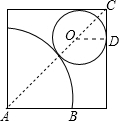
解答:解:如图易得AC=
=46
,
设小圆的半径为r,
∴小圆的周长为2πr,
∵在一边长为46cm的正方形纸片上剪下一块圆形和一个扇形纸片,
∴△OCD是等直角三角形,则OC=
r.
设大圆的半径为x,
则
=2πr,
解得x=4r.
∵4r+r+
r=46
,
解得r=10
-4.
故答案为:(10
-4).
| 462+462 |
| 2 |

设小圆的半径为r,
∴小圆的周长为2πr,
∵在一边长为46cm的正方形纸片上剪下一块圆形和一个扇形纸片,
∴△OCD是等直角三角形,则OC=
| 2 |
设大圆的半径为x,
则
| 90π×x |
| 180 |
解得x=4r.
∵4r+r+
| 2 |
| 2 |
解得r=10
| 2 |
故答案为:(10
| 2 |
点评:本题考查了圆锥的计算,根据正方形的对角线长得到相应的关系式是解决本题的关键.

练习册系列答案
相关题目
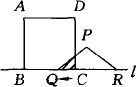
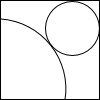 如图所示:在一边长为46cm的正方形纸片上剪下一块圆形和一个扇形纸片,使之恰好做成一个圆锥形模型,它的底面半径是________cm.
如图所示:在一边长为46cm的正方形纸片上剪下一块圆形和一个扇形纸片,使之恰好做成一个圆锥形模型,它的底面半径是________cm.