题目内容
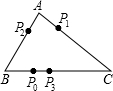 电子跳蚤游戏盘(如图)为△ABC,AB=8,AC=9,BC=10,如果电子跳蚤开始时在BC边一的P0点,BP0=4.第一步跳蚤跳到AC边上P1点,且CP1=CP0;第二步跳蚤从P1跳到AB边上P2点,且AP2=AP1;第三步跳蚤从P2 跳回到BC边上P3点,且BP3=BP2;…跳蚤按上述规则跳下去,第2003次落点为P2003,则P3与P2003之间的距离为
电子跳蚤游戏盘(如图)为△ABC,AB=8,AC=9,BC=10,如果电子跳蚤开始时在BC边一的P0点,BP0=4.第一步跳蚤跳到AC边上P1点,且CP1=CP0;第二步跳蚤从P1跳到AB边上P2点,且AP2=AP1;第三步跳蚤从P2 跳回到BC边上P3点,且BP3=BP2;…跳蚤按上述规则跳下去,第2003次落点为P2003,则P3与P2003之间的距离为分析:此题首先根据题意,分别计算电子跳骚的位置和三角形的顶点的距离,找到循环的规律:经过6次跳,电子跳蚤回到起跳点.根据这一规律确定第2003次落点的位置,再根据△BP3P2003∽△BCA,从而确定P3与P2010之间的距离.
解答:解:∵BC=10,BP0=4,知CP0=6,
∴CP1=6.
∵AC=9,
∴AP2=AP1=3.
∵AB=8,
∴BP3=BP2=5.
∴CP4=CP3=5,
∴AP4=4.
∴AP5=AP4=4,
∴BP5=4.
∴BP6=BP5=4.
此时P6与P0重合,即经过6次跳,电子跳蚤回到起跳点.
2003÷6=333…5,即P2003与P5重合,
可证△BP3P2003∽△BCA,
此时P3与P2003之间的距离是
AC=4.5.
故答案为:4.5.
∴CP1=6.
∵AC=9,
∴AP2=AP1=3.
∵AB=8,
∴BP3=BP2=5.
∴CP4=CP3=5,
∴AP4=4.
∴AP5=AP4=4,
∴BP5=4.
∴BP6=BP5=4.
此时P6与P0重合,即经过6次跳,电子跳蚤回到起跳点.
2003÷6=333…5,即P2003与P5重合,
可证△BP3P2003∽△BCA,
此时P3与P2003之间的距离是
| 1 |
| 2 |
故答案为:4.5.
点评:本题考查了规律型:图形的变化和相似三角形的判定和性质,此题主要是能够根据题意正确计算出有关线段的长,发现电子跳蚤的落点的循环规律,从而完成计算.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
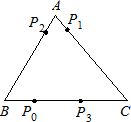 8、电子跳蚤游戏盘是如图所示的△ABC,AB=6,AC=7,BC=8.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;…;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2007与P2010之间的距离为( )
8、电子跳蚤游戏盘是如图所示的△ABC,AB=6,AC=7,BC=8.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;…;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2007与P2010之间的距离为( ) (2012•椒江区二模)电子跳蚤游戏盘是如图所示的△ABC,AB=6,AC=7,BC=8.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;…;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2012与P2015之间的距离为( )
(2012•椒江区二模)电子跳蚤游戏盘是如图所示的△ABC,AB=6,AC=7,BC=8.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;…;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2012与P2015之间的距离为( ) 如图,电子跳蚤游戏盘是如图所示的△ABC,AB=AC=BC=6.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2011与点P2012之间的距离为
如图,电子跳蚤游戏盘是如图所示的△ABC,AB=AC=BC=6.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2011与点P2012之间的距离为