题目内容
 电子跳蚤游戏盘是如图所示的△ABC,AB=AC=BC=6.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;…;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点B与点P12之间的距离为( )
电子跳蚤游戏盘是如图所示的△ABC,AB=AC=BC=6.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;…;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点B与点P12之间的距离为( )分析:由于AB=AC=BC=6,BP0=2,CP1=CP0;AP2=AP1;BP3=BP2得到点P0、点P1、点P2、点P3都是△ABC各边的三等份点,继续这个过程得到第四步从P3跳到CA边的P4(第四次落点)处,且CP4=CP3;第五步从P4跳到AB边的P5(第五次落点)处,且AP5=AP4;第六步从P5跳到BC边的P0(第四次落点)处,且BP0=BP5,即点P6与点P0重合,即从第六次开始重复前面的过程,并且每六次一循环,由此得到点P12落在点P0处,则点B与点P12之间的距离=BP0=2.
解答:解:如图,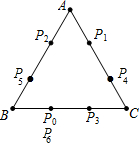
∵AB=AC=BC=6,BP0=2,CP1=CP0;AP2=AP1;BP3=BP2;
∴点P0、点P1、点P2、点P3都是△ABC各边的三等份点,
∴第四步从P3跳到CA边的P4(第四次落点)处,且CP4=CP3;第五步从P4跳到AB边的P5(第五次落点)处,且AP5=AP4;第六步从P5跳到BC边的P0(第四次落点)处,且BP0=BP5;
∴从第六次开始重复前面的过程,并且每六次一循环,
∴点P12落在点P0处,
∴点B与点P12之间的距离=BP0=2.
故选A.

∵AB=AC=BC=6,BP0=2,CP1=CP0;AP2=AP1;BP3=BP2;
∴点P0、点P1、点P2、点P3都是△ABC各边的三等份点,
∴第四步从P3跳到CA边的P4(第四次落点)处,且CP4=CP3;第五步从P4跳到AB边的P5(第五次落点)处,且AP5=AP4;第六步从P5跳到BC边的P0(第四次落点)处,且BP0=BP5;
∴从第六次开始重复前面的过程,并且每六次一循环,
∴点P12落在点P0处,
∴点B与点P12之间的距离=BP0=2.
故选A.
点评:本题考查了规律型:图形的变化类:通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
相关题目
 18、电子跳蚤游戏盘是如图所示的△ABC,AB=AC=BC=6.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2009与点P2010之间的距离为
18、电子跳蚤游戏盘是如图所示的△ABC,AB=AC=BC=6.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2009与点P2010之间的距离为 12、电子跳蚤游戏盘是如图所示的△ABC,AB=6,AC=7,BC=8.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第一次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第一次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第三次落点)处,且BP3=BP2;…;跳蚤按上述规则一致跳下去,第n次落点为Pn(n为正整数),则点P2007与P2010之间的距离为
12、电子跳蚤游戏盘是如图所示的△ABC,AB=6,AC=7,BC=8.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第一次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第一次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第三次落点)处,且BP3=BP2;…;跳蚤按上述规则一致跳下去,第n次落点为Pn(n为正整数),则点P2007与P2010之间的距离为 (2012•椒江区二模)电子跳蚤游戏盘是如图所示的△ABC,AB=6,AC=7,BC=8.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;…;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2012与P2015之间的距离为( )
(2012•椒江区二模)电子跳蚤游戏盘是如图所示的△ABC,AB=6,AC=7,BC=8.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;…;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2012与P2015之间的距离为( )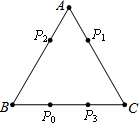 电子跳蚤游戏盘是如图所示的△ABC,AB=AC=BC=6.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2010与点P2011之间的距离为
电子跳蚤游戏盘是如图所示的△ABC,AB=AC=BC=6.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2010与点P2011之间的距离为