Question

【题目】如图，等腰Rt△ABP的斜边AB=2，点M、N在斜边AB上．若△PMN是等腰三角形且底角正切值为2，则MN＝_________．

Answer 1

【答案】1或

【解析】

分MN是底边与MP是底边，分别作图，根据等腰三角形的性质及正切的定义即可求解．

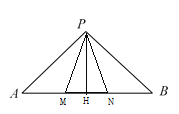
如图，当MN是底边的等腰△PMN时

作PH⊥AB，∵△PAB是等腰直角三角形，

∴PH=AH=BH=AB=1

∵△PMN是等腰三角形且底角正切值为2，

故tan∠PMN=2

即

解得MH=

∴MN=2MH=1；

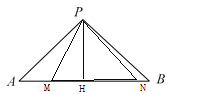
如图，当MP是底边的等腰△PMN时,

作PH⊥AB，∵△PAB是等腰直角三角形，

∴PH=AH=BH=AB=1

∵△PMN是等腰三角形且底角正切值为2，

故tan∠PMN=2

∴MH=

设PN=MN=x，则HN=x-

∵PN2=PH2+HN2

即x2=12+( x-)2

解得x=,

综上，MN＝1或

故答案为：1或．