题目内容
阅读下列材料,然后回答问题.
在进行二次根式计算时,我们有时会碰到如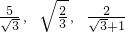 一样的式子,其实我们还可以将其进一步简化:
一样的式子,其实我们还可以将其进一步简化: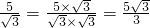 ①
①
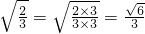 ②
②
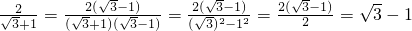 ③
③
以上这种化简的步骤叫做分母有理化,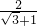 还可以用以下方法化简:
还可以用以下方法化简: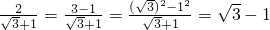 ④
④
(1)请用不同的方法化简: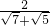
参照③式方法化简过程为:
参照④式方法化简过程为:
(2)化简: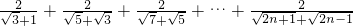 .
.
解:(1):参照③式方法化简过程为:原式=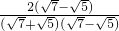 =
= -
- ;
;
参照④式方法化简过程为:原式=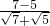 =
= =
= -
- .
.
(2)原式= -1+
-1+ -
- +
+ -
- +…+
+…+ -
- =
= -1.
-1.
分析:(1)根据已知中的例子,③的方式是:分子、分母上同时乘以与分母构成平方差公式的式子,从而化简;
④的方式是:把2化成两个数的差,利用平方差公式分解,然后约分;
(2)根据(1)的结论,直接运用计算即可.
点评:本题主要考查了二次根式的化简,正确读懂题意是解题的关键.
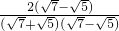 =
= -
- ;
;参照④式方法化简过程为:原式=
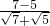 =
= =
= -
- .
.(2)原式=
 -1+
-1+ -
- +
+ -
- +…+
+…+ -
- =
= -1.
-1.分析:(1)根据已知中的例子,③的方式是:分子、分母上同时乘以与分母构成平方差公式的式子,从而化简;
④的方式是:把2化成两个数的差,利用平方差公式分解,然后约分;
(2)根据(1)的结论,直接运用计算即可.
点评:本题主要考查了二次根式的化简,正确读懂题意是解题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目