题目内容
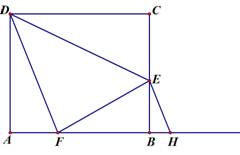
(本题14分)如图,矩形ABCD中,AB=12,AD=9,E为BC上一点,且BE=4,动点F从点A出发沿射线AB方向以每秒3个单位的速度运动.连结DF,DE, EF. 过点E作DF的平行线交射线AB于点H,设点F的运动时间为t(不考虑D、E、F在一条直线上的情况).
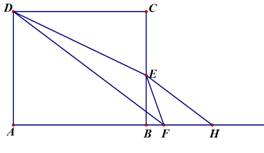
1.(1) 填空:当t= 时,AF=CE,此时BH= ;
2.(2)当△BEF与△BEH相似时,求t的值;
3.(3)当F在线段AB上时,设△DEF的面积为S,△DEF的周长为C.
① 求S关于t的函数关系式;
② 直接写出C的最小值.
【答案】
1.(1) 填空:当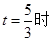 ,(1分)AF=CE,
此时
,(1分)AF=CE,
此时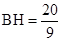 ;(2分)
;(2分)
2.(2)由EH∥DF得∠AFD=∠BHE,又∵∠A=∠CBH=90°
∴△EBH∽△DAF ∴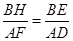 即
即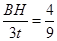 ∴BH=
∴BH=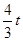 (2分)
(2分)
当点F在点B的左边时,即t<4时,BF=12-3t
此时,当△BEF∽△BHE时: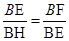 即
即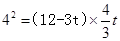 解得:
解得: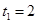 (1分)
(1分)
此时,当△BEF∽△BEH时: 有BF=BH, 即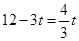 解得:
解得: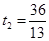 (1分)
(1分)
当点F在点B的右边时,即t>4时,BF=3t-12
此时,当△BEF∽△BHE时: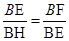 即
即 解得:
解得: (2分)
(2分)
3.(3)① ∵EH∥DF
∴△DFE的面积=△DFH的面积=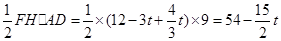 (3分)
(3分)
(其他解法若正确,酌情给分)
② 直接写出C的最小值= (2分)
(2分)
【解析】略

练习册系列答案
相关题目

 ,求
,求 的值和这个一次函数的解析式;
的值和这个一次函数的解析式; (3)探究:在BC边上是否存在点M使得四边形PDQM是菱形?若存在,请找出点M,并求出BM的长;不存在,请说明理由.
(3)探究:在BC边上是否存在点M使得四边形PDQM是菱形?若存在,请找出点M,并求出BM的长;不存在,请说明理由. ,AC=BC=2,M是边AC的中点,
,AC=BC=2,M是边AC的中点,

