题目内容
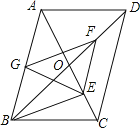
【题目】如图，平行四边形ABCD中，对角线AC、BD相交于O，BD=2AD，E、F、G分别是OC、OD、AB的中点，下列结论：①BE⊥AC；②EG=GF；③△EFG≌△GBE；④EA平分∠GEF；⑤四边形BEFG是菱形．其中正确的是（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
由平行四边形的性质可得OB=BC，由等腰三角形的性质可判断①正确，由直角三角形的性质和三角形中位线定理可判断②错误，通过证四边形BGFE是平行四边形，可判断③正确，由平行线的性质和等腰三角形的性质可判断④正确，由∠BAC≠30°可判断⑤错误．
∵四边形ABCD是平行四边形
∴BO=DO=
BD，AD=BC，AB=CD，AB∥BC，
又∵BD=2AD，
∴OB=BC=OD=DA，且点E 是OC中点，
∴BE⊥AC，
故①正确，
∵E、F分别是OC、OD的中点，
∴EF∥CD，EF=CD，
∵点G是Rt△ABE斜边AB上的中点，
∴GE=AB=AG=BG
∴EG=EF=AG=BG，无法证明GE=GF，
故②错误，
∵BG=EF，AB∥CD∥EF
∴四边形BGFE是平行四边形，
∴GF=BE，且BG=EF，GE=GE，
∴△BGE≌△FEG（SSS）
故③正确
∵EF∥CD∥AB，
∴∠BAC=∠ACD=∠AEF，
∵AG=GE，
∴∠GAE=∠AEG，
∴∠AEG=∠AEF，
∴AE平分∠GEF，
故④正确，
若四边形BEFG是菱形
∴BE=BG=AB，
∴∠BAC=30°
与题意不符合
故⑤错误
故选B．
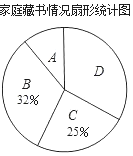
【题目】在“书香校园”活动中，某校为了解学生家庭藏书情况，随机抽取本校部分学生进行调查，并绘制成部分统计图表如下：
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤100 | a |
C | 101≤m≤200 | 50 |
D | m≥201 | 66 |
根据以上信息，解答下列问题：
(1)该调查的样本容量为_____，a＝_____；
(2)在扇形统计图中，“A”对应扇形的圆心角为_____°；
(3)若该校有2000名学生，请估计全校学生中家庭藏书200本以上的人数．
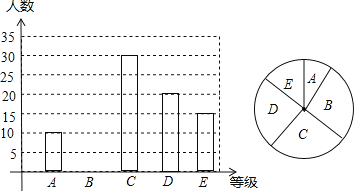
【题目】2019年，我省中考体育分值增加到55分，其中女生必考项目为八百米跑，我校现抽取九年级部分女生进行八百米测试成绩如下：
成绩 | 3′40″及以下 | 3′41～4′ | 4′01″～4′20′ | 4′21″～4′40″ | 4′41″及以上 |
等级 | A | B | C | D | E |
百分比 | 10% | 25% | m | 20% | n |
（1）求样本容量及表格中的m和n的值
（2）求扇形统计图中A等级所对的圆心角度数，并补全统计图．
（3）我校9年级共有女生500人．若女生八百米成绩的达标成绩为4分，我校九年级女生八百米成绩达标的人数有多少？
