题目内容
 已知,如图AP=7.2,CP=3.5,DP=4.5,BP=5.6,说明AB∥CD.
已知,如图AP=7.2,CP=3.5,DP=4.5,BP=5.6,说明AB∥CD.
证明:∵AP=7.2,CP=3.5,DP=4.5,BP=5.6,
∴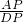 =
=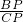 =
= ;
;
∵∠APB=∠DPC(对顶角相等),
∴△APB∽△DPC(SAS),
∴∠B=∠C(相似三角形的对应角相等),
∴AB∥CD(内错角相等,两直线平行).
分析:根据相似三角形的判定定理SAS判定△APB∽△DPC,然后由相似三角形的对应角相等推知内错角∠B=∠C;最后由内错角相等证得两直线平行,即AB∥CD.
点评:本题考查了相似三角形的判定与性质.相似三角形的判定定理:
(1)两角对应相等的两个三角形相似(AA).
(2)两边对应成比例且夹角相等的两个三角形相似(SAS).
(3)三边对应成比例的两个三角形相似(SSS).
∴
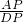 =
=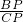 =
= ;
;∵∠APB=∠DPC(对顶角相等),
∴△APB∽△DPC(SAS),
∴∠B=∠C(相似三角形的对应角相等),
∴AB∥CD(内错角相等,两直线平行).
分析:根据相似三角形的判定定理SAS判定△APB∽△DPC,然后由相似三角形的对应角相等推知内错角∠B=∠C;最后由内错角相等证得两直线平行,即AB∥CD.
点评:本题考查了相似三角形的判定与性质.相似三角形的判定定理:
(1)两角对应相等的两个三角形相似(AA).
(2)两边对应成比例且夹角相等的两个三角形相似(SAS).
(3)三边对应成比例的两个三角形相似(SSS).

练习册系列答案
相关题目
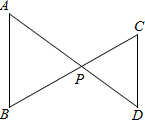 已知,如图AP=7.2,CP=3.5,DP=4.5,BP=5.6,说明AB∥CD.
已知,如图AP=7.2,CP=3.5,DP=4.5,BP=5.6,说明AB∥CD.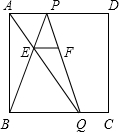 EF平行BC交PQ于F,AP、BQ分别为方程x2-mx+n=0的两根.
EF平行BC交PQ于F,AP、BQ分别为方程x2-mx+n=0的两根.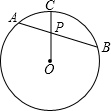 (1998•河北)已知:如图弦AB经过⊙O的半径OC的中点P,且AP=2,PB=3,则是⊙O的半径等于( )
(1998•河北)已知:如图弦AB经过⊙O的半径OC的中点P,且AP=2,PB=3,则是⊙O的半径等于( )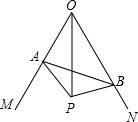 (2013•海门市一模)已知,如图,∠MON=60°,点A、B为射线OM,ON上的动点,且AB=4
(2013•海门市一模)已知,如图,∠MON=60°,点A、B为射线OM,ON上的动点,且AB=4