题目内容
【题目】如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接AF交对角线于点E,连接EC 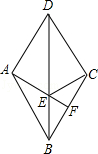
(1)求证:AE=EC;
(2)当∠ABC=60°,∠CEF=60°时,点F在线段BC的什么位置?说明理由.
【答案】
(1)证明:连接AC.
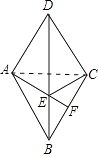
∵BD是菱形ABCD的对角线,
∴BD垂直平分AC,
∴AE=EC
(2)解:点F是线段BC的中点.
理由:∵四边形ABCD是菱形,
∴AB=CB.
又∵∠ABC=60°,
∴△ABC是等边三角形,
∴∠BAC=60°.
∵AE=EC,
∴∠EAC= ![]() ∠CEF=30°.
∠CEF=30°.
又∵∠BAF=∠BAC﹣∠EAC=30°=∠EAC,
∴AF是等边△ABC的角平分线,
∴BF=CF,
∴点F是线段BC的中点
【解析】(1)利用菱形的对角线互相垂直平分即可证明;(2)首先证明△ABC是等边三角形,再证明AF是等边△ABC的角平分线即可;
【考点精析】解答此题的关键在于理解菱形的性质的相关知识,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目