题目内容

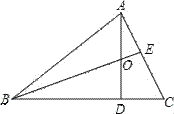
【题目】△ABC中，AD⊥BC于点D，BE是∠ABC的平分线，已知∠ABC=40°，∠C=60°，求∠AOB的度数.

【答案】110°

【解析】

由三角形内角和定理可求得∠BAC的度数．在Rt△ADC中可求得∠DAC的度数，故有∠BAO=∠BAC﹣∠DAC，而∠ABO=∠ABC，则在△ABO中，可由三角形内角和定理求得∠AOB的度数．

∵∠ABC=40°，∠C=60°，∴∠BAC=180°﹣40°﹣60°=80°．

∵AD⊥BC，∠C=60°，∴∠DAC=30°，∴∠BAO=∠BAC﹣∠DAC=50°．

∵BE是∠ABC的平分线，∠ABC=40°，∴∠ABO=∠ABC=20°，∴∠AOB=180°﹣∠ABO﹣∠BAO=110°．

练习册系列答案
相关题目

【题目】如图，△ABC中，AC＝8，AB＝10，△ABC的面积为30，AD平分∠BAC，F、E分别为AC、AD上两动点，连接CE、EF，则CE＋EF的最小值为_______

【题目】如图，抛物线y＝ax2＋bx＋c与x轴交于A，B两点(点A在点B左侧)，与y轴交于点C，且当x＝0和x＝2时，y的值相等，直线y＝3x－7与这条抛物线交于两点，其中一点横坐标为4，另一点是这条抛物线的顶点M.

(1)求顶点M的坐标．

(2)求这条抛物线对应的函数解析式．

(3)P为线段BM上一点(P不与点B，M重合)，作PQ⊥x轴于点Q，连接PC，设OQ＝t，四边形PQAC的面积为S，求S与t的函数解析式，并直接写出t的取值范围．

(4)在线段BM上是否存在点N，使△NMC为等腰三角形？若存在，求出点N的坐标，若不存在，说明理由．

【题目】某商店购进600个旅游纪念品，进价为每个6元，第一周以每个10元的价格售出200个，第二周若按每个10元的价格销售仍可售出200个，但商店为了适当增加销量，决定降价销售（根据市场调查，单价每降低1元，可多售出50个，但售价不得低于进价），单价降低x元销售销售一周后，商店对剩余旅游纪念品清仓处理，以每个4元的价格全部售出，如果这批旅游纪念品共获利1250元，问第二周每个旅游纪念品的销售价格为多少元？

【题目】已知：如图，抛物线y＝ax2＋bx＋c与x轴交于点A(2，0)，B(4，0)，且过点C(0，4)．

(1)求出抛物线的表达式和顶点坐标；

(2)请你求出抛物线向左平移3个单位长度，再向上平移1.5个单位长度后抛物线的表达式．

【题目】如图，在中，,垂足为，为直线上一动点(不与点重合)，在的右侧作，使得,连接．

（1）求证：；

（2）当在线段上时

① 求证：≌；

② 若, 则；

（3）当CE∥AB时，若△ABD中最小角为20°，试探究∠ADB的度数（直接写出结果）

【题目】（1）如图①，，射线在这个角的内部，点、分别在的边、上，且，于点，于点．求证：；

（2）如图②，点、分别在的边、上，点、都在内部的射线上，、分别是、的外角．已知，且．求证：；

（3）如图③，在中，，．点在边上，，点、在线段上，．若的面积为15，求与的面积之和．

【题目】如图，四边形ABCD中，AB＝AD，AC＝5，∠DAB＝∠DCB＝90°，则四边形ABCD的面积为( )

A.25B.12.5C.5D.10

【题目】综合与实践：

问题情境：

在数学综合与实践课上，张老师启示大家利用直线、线段以及点的运动变换进行探究活动.变换条件如下：如图 1，直线 AB，AC，BC 两两相交于 A，B，C 三点，得知△ABC是等边三角形，点 E 是直线 AC 上一动点（点 E 不与点 A，C 重合），点 F 在直线 BC上，连接 BE，EF，使 EF=BE．

独立思考：

（1）张老师首先提出了这样一个问题：如图 1，当E是线段 AC 的中点时，确定线段 AE与 CF 的数量关系，请你直接写出结论：AE____ CF（填“＞” “＜”或“=”）.

提出问题：

（2）“奋斗”小组受此问题的启发，提出问题：若点E是线段 AC 上的任意一点，其他条件不变，（1）中的结论是否成立？该小组认为结论仍然成立，理由如下：如图 2，过点 E作 ED∥BC，交 AB 于点 D. （请你补充完整证明过程）

拓展延伸：

（3）“缜密”小组提出的问题是：动点E的运动位置如图3，图4所示，其他条件不变，根据题意补全图形，并判断线段AE与CF的数量关系是否发生变化？ 请你选择其中一种予以证明.

（4）“爱心”小组提出的问题是：若等边△ABC 的边长为 ，AE=1，则BF 的长为__________.（请你直接写出结果）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网