题目内容
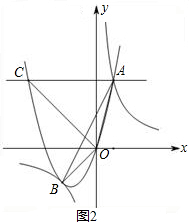
直线l:y=- x+3分别交x轴、y轴于B、A两点,等腰直角△CDM斜边落在x轴上,且CD=6,如图1所示.若直线l以每秒3个单位向上作匀速平移运动,同时点C从(6,0)开始以每秒2个单位的速度向右作匀速平移运动,如图2所示,设移动后直线l运动后分别交x轴、y轴于Q、P两点,以OP、OQ为边作如图矩形OPRQ.设运动时间为t秒.
x+3分别交x轴、y轴于B、A两点,等腰直角△CDM斜边落在x轴上,且CD=6,如图1所示.若直线l以每秒3个单位向上作匀速平移运动,同时点C从(6,0)开始以每秒2个单位的速度向右作匀速平移运动,如图2所示,设移动后直线l运动后分别交x轴、y轴于Q、P两点,以OP、OQ为边作如图矩形OPRQ.设运动时间为t秒.
(1)求运动后点M、点Q的坐标(用含t的代数式表示);
(2)若设矩形OPRQ与运动后的△CDM的重叠部分面积为S,求S与t的函数关系式,并写出t相应的取值范围;
(3)若直线l和△CDM运动后,直线l上存在点T使∠OTC=90°,则当在线段PQ上符合条件的点T有且只有两个时,求t的取值范围.
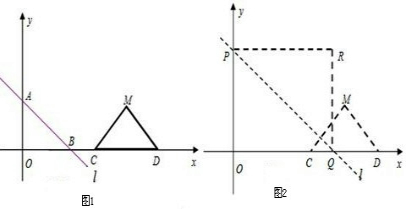
(1)解:过M作MN⊥CD于N,
∵等腰直角△CDM,
∴CN=DN=MN=3,
由勾股定理得:MC=MD=3 ,
,
∵点C从(6,0)开始以每秒2个单位的速度向右作匀速平移运动,
∴ON=6+3+2t=9+2t,
∵y=- x+3,
x+3,
∴当y=0时,x=4,
∴B(4,0),
∵直线l以每秒3个单位向上作匀速平移运动,
∴直线PQ的解析式是y=- x+3+3t,
x+3+3t,
y=0代入得:0=- x+3+3t,
x+3+3t,
x=4t+4
∴OQ=4+4t,
∴M(9+2t,3),Q(4+4t,0),
答:运动后点M、点Q的坐标分别是(9+2t,3),(4+4t,0).
(2)解:①∵当两图形不重合时,OB=3,OC=6,直线l以每秒3个单位向上作匀速平移运动,同时点C从(6,0)开始以每秒2个单位的速度向右作匀速平移运动
∴0<t<1,s=0,如图1,
②∵当t=2.5时,RQ过M点,
∴1<t≤2.5,如图2,由矩形OPRQ,∠OQH=90°,
∵∠MCD=45°=∠CHQ,
∴CQ=(4+4t)-(6+2t)=2t-2=QH,
∴S= CQ•QH=
CQ•QH= (2t-2)2=2t2-4t+2,
(2t-2)2=2t2-4t+2,
即:s=2t2-4t+2;
③∵当t=4时,RQ过D点,
∴当2.5<t<4时,如图(3):
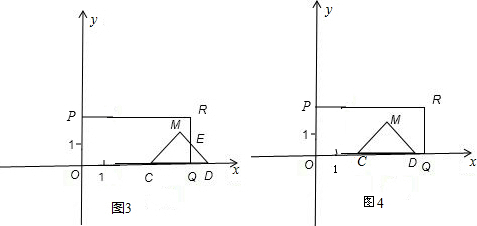
同法可求DQ=OD-OQ=(6+6+2t)-(4+4t)=8-2t,
∴s=S△CMD-S△DQE= ×6×3-
×6×3- (8-2t)2=-2t2+16t-23,
(8-2t)2=-2t2+16t-23,
即:s=-2t2+16t-23;
④∵当t≥4时,△MDC在矩形PRQO的内部,
∴当t≥4时,s=S△CMD= ×6×3=9;
×6×3=9;
答:S与t的函数关系式是s=2t2-4t+2(1<t≤2.5)或s=-2t2+16t-23(2.5<t<4)或s=9(t≥4).
(3)解:①直线L经过点C,即C、Q重合
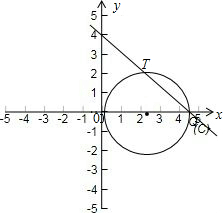
此时4+4t=6+2t,
解得:t=1;
②如图直线L切圆于F,即点T,OE=EF=3+t,EQ=1+3t
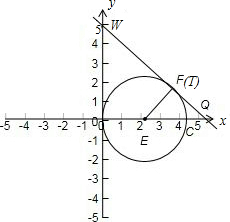
∵∠FQC=∠FQC,∠EFQ=∠COW=90°,
∴△QFE∽△QOW,
∴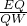 =
= ,
,
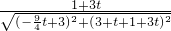 =
=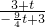 ,
,
求得:t=3,
∴1<t<3,
答:t的取值范围是1<t<3.
分析:(1)过M作MN⊥CD于N,根据等腰直角三角形的性质求出CN=DN=MN=3,求出B的坐标,即可得到M、Q的坐标;
(2)①0<t<1时,s=0②1<t≤2.5,如图2,S= CQ•QH,把CQ、QH代入即可求出答案;③当2.5<t<4时,如图(3)同法可求DQ,根据s=S△CMD-S△DQE,求出△CMD和△DQE的面积代入即可;④当t≥4时,s=S△CMD=
CQ•QH,把CQ、QH代入即可求出答案;③当2.5<t<4时,如图(3)同法可求DQ,根据s=S△CMD-S△DQE,求出△CMD和△DQE的面积代入即可;④当t≥4时,s=S△CMD= ×6×3=9;
×6×3=9;
(3)①直线L经过点C,即C、Q重合,根据4+4t=6+2t,求出即可;②如图直线L切圆于F,证△QFE∽△QOW,得出
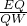 =
= ,代入即可求出t的值,进一步得出t的取值范围.
,代入即可求出t的值,进一步得出t的取值范围.
点评:本题主要考查对矩形的性质,相似三角形的性质和判定,等腰三角形的性质和判定,三角形的面积,勾股定理,一次函数的性质,解一元一次方程,等腰直角三角形的性质,三角形的内角和定理等知识点的理解和掌握,此题是一个综合性比较强的题目,有一定的难度,用的数学思想是分类讨论思想.
∵等腰直角△CDM,
∴CN=DN=MN=3,
由勾股定理得:MC=MD=3
 ,
,∵点C从(6,0)开始以每秒2个单位的速度向右作匀速平移运动,

∴ON=6+3+2t=9+2t,
∵y=-
 x+3,
x+3,∴当y=0时,x=4,
∴B(4,0),
∵直线l以每秒3个单位向上作匀速平移运动,
∴直线PQ的解析式是y=-
 x+3+3t,
x+3+3t,y=0代入得:0=-
 x+3+3t,
x+3+3t,x=4t+4
∴OQ=4+4t,
∴M(9+2t,3),Q(4+4t,0),
答:运动后点M、点Q的坐标分别是(9+2t,3),(4+4t,0).

(2)解:①∵当两图形不重合时,OB=3,OC=6,直线l以每秒3个单位向上作匀速平移运动,同时点C从(6,0)开始以每秒2个单位的速度向右作匀速平移运动
∴0<t<1,s=0,如图1,
②∵当t=2.5时,RQ过M点,
∴1<t≤2.5,如图2,由矩形OPRQ,∠OQH=90°,
∵∠MCD=45°=∠CHQ,
∴CQ=(4+4t)-(6+2t)=2t-2=QH,
∴S=
 CQ•QH=
CQ•QH= (2t-2)2=2t2-4t+2,
(2t-2)2=2t2-4t+2,即:s=2t2-4t+2;
③∵当t=4时,RQ过D点,
∴当2.5<t<4时,如图(3):

同法可求DQ=OD-OQ=(6+6+2t)-(4+4t)=8-2t,
∴s=S△CMD-S△DQE=
 ×6×3-
×6×3- (8-2t)2=-2t2+16t-23,
(8-2t)2=-2t2+16t-23,即:s=-2t2+16t-23;
④∵当t≥4时,△MDC在矩形PRQO的内部,
∴当t≥4时,s=S△CMD=
 ×6×3=9;
×6×3=9;答:S与t的函数关系式是s=2t2-4t+2(1<t≤2.5)或s=-2t2+16t-23(2.5<t<4)或s=9(t≥4).
(3)解:①直线L经过点C,即C、Q重合

此时4+4t=6+2t,
解得:t=1;
②如图直线L切圆于F,即点T,OE=EF=3+t,EQ=1+3t

∵∠FQC=∠FQC,∠EFQ=∠COW=90°,
∴△QFE∽△QOW,
∴
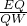 =
= ,
,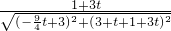 =
=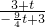 ,
,求得:t=3,
∴1<t<3,
答:t的取值范围是1<t<3.
分析:(1)过M作MN⊥CD于N,根据等腰直角三角形的性质求出CN=DN=MN=3,求出B的坐标,即可得到M、Q的坐标;
(2)①0<t<1时,s=0②1<t≤2.5,如图2,S=
 CQ•QH,把CQ、QH代入即可求出答案;③当2.5<t<4时,如图(3)同法可求DQ,根据s=S△CMD-S△DQE,求出△CMD和△DQE的面积代入即可;④当t≥4时,s=S△CMD=
CQ•QH,把CQ、QH代入即可求出答案;③当2.5<t<4时,如图(3)同法可求DQ,根据s=S△CMD-S△DQE,求出△CMD和△DQE的面积代入即可;④当t≥4时,s=S△CMD= ×6×3=9;
×6×3=9;(3)①直线L经过点C,即C、Q重合,根据4+4t=6+2t,求出即可;②如图直线L切圆于F,证△QFE∽△QOW,得出
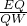 =
= ,代入即可求出t的值,进一步得出t的取值范围.
,代入即可求出t的值,进一步得出t的取值范围.点评:本题主要考查对矩形的性质,相似三角形的性质和判定,等腰三角形的性质和判定,三角形的面积,勾股定理,一次函数的性质,解一元一次方程,等腰直角三角形的性质,三角形的内角和定理等知识点的理解和掌握,此题是一个综合性比较强的题目,有一定的难度,用的数学思想是分类讨论思想.

练习册系列答案
相关题目
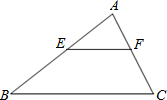 如图,在△ABC中,AE=EB,AF=FC,有一同学发现EF与BC存在以下关系:EF∥BC,且EF=
如图,在△ABC中,AE=EB,AF=FC,有一同学发现EF与BC存在以下关系:EF∥BC,且EF=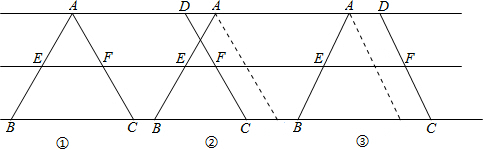

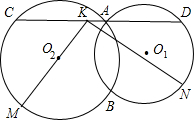 如图,⊙O1与⊙O2相交于点A和B,经过A作直线与⊙O1相交于D,与⊙O2相交于C,设弧BC的中点为M,弧BD的中点为N,线段CD的中点为K.求证:MK⊥KN.
如图,⊙O1与⊙O2相交于点A和B,经过A作直线与⊙O1相交于D,与⊙O2相交于C,设弧BC的中点为M,弧BD的中点为N,线段CD的中点为K.求证:MK⊥KN.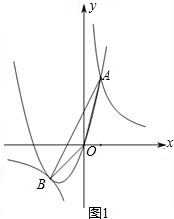
 函数
函数 25、已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
25、已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.