题目内容
(2007•无锡)任何一个正整数n都可以进行这样的分解:n=s×t(s,t是正整数,且s≤t),如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:F(n)=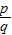 .例如18可以分解成1×18,2×9,3×6这三种,这时就有F(18)=
.例如18可以分解成1×18,2×9,3×6这三种,这时就有F(18)= =
= .给出下列关于F(n)的说法:(1)F(2)=
.给出下列关于F(n)的说法:(1)F(2)= ;(2)F(24)=
;(2)F(24)= ;(3)F(27)=3;(4)若n是一个完全平方数,则F(n)=1.其中正确说法的个数是( )
;(3)F(27)=3;(4)若n是一个完全平方数,则F(n)=1.其中正确说法的个数是( )A.1
B.2
C.3
D.4
【答案】分析:把2,24,27,n分解为两个正整数的积的形式,找到相差最少的两个数,让较小的数除以较大的数,看结果是否与所给结果相同.
解答:解:∵2=1×2,
∴F(2)= 是正确的;
是正确的;
∵24=1×24=2×12=3×8=4×6,这几种分解中4和6的差的绝对值最小,
∴F(24)= =
= ,故(2)是错误的;
,故(2)是错误的;
∵27=1×27=3×9,其中3和9的绝对值较小,又3<9,
∴F(27)= ,故(3)是错误的;
,故(3)是错误的;
∵n是一个完全平方数,
∴n能分解成两个相等的数,则F(n)=1,故(4)是正确的.
∴正确的有(1),(4).
故选B.
点评:本题考查题目信息获取能力,解决本题的关键是理解此题的定义:所有这种分解中两因数之差的绝对值最小,F(n)=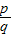 (p≤q).
(p≤q).
解答:解:∵2=1×2,
∴F(2)=
 是正确的;
是正确的;∵24=1×24=2×12=3×8=4×6,这几种分解中4和6的差的绝对值最小,
∴F(24)=
 =
= ,故(2)是错误的;
,故(2)是错误的;∵27=1×27=3×9,其中3和9的绝对值较小,又3<9,
∴F(27)=
 ,故(3)是错误的;
,故(3)是错误的;∵n是一个完全平方数,
∴n能分解成两个相等的数,则F(n)=1,故(4)是正确的.
∴正确的有(1),(4).
故选B.
点评:本题考查题目信息获取能力,解决本题的关键是理解此题的定义:所有这种分解中两因数之差的绝对值最小,F(n)=
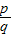 (p≤q).
(p≤q). 
练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
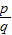 .例如18可以分解成1×18,2×9,3×6这三种,这时就有F(18)=
.例如18可以分解成1×18,2×9,3×6这三种,这时就有F(18)= =
= .给出下列关于F(n)的说法:(1)F(2)=
.给出下列关于F(n)的说法:(1)F(2)= ;(2)F(24)=
;(2)F(24)= ;(3)F(27)=3;(4)若n是一个完全平方数,则F(n)=1.其中正确说法的个数是( )
;(3)F(27)=3;(4)若n是一个完全平方数,则F(n)=1.其中正确说法的个数是( )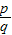 .例如18可以分解成1×18,2×9,3×6这三种,这时就有F(18)=
.例如18可以分解成1×18,2×9,3×6这三种,这时就有F(18)= =
= .给出下列关于F(n)的说法:(1)F(2)=
.给出下列关于F(n)的说法:(1)F(2)= ;(2)F(24)=
;(2)F(24)= ;(3)F(27)=3;(4)若n是一个完全平方数,则F(n)=1.其中正确说法的个数是( )
;(3)F(27)=3;(4)若n是一个完全平方数,则F(n)=1.其中正确说法的个数是( )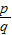 .例如18可以分解成1×18,2×9,3×6这三种,这时就有F(18)=
.例如18可以分解成1×18,2×9,3×6这三种,这时就有F(18)= =
= .给出下列关于F(n)的说法:(1)F(2)=
.给出下列关于F(n)的说法:(1)F(2)= ;(2)F(24)=
;(2)F(24)= ;(3)F(27)=3;(4)若n是一个完全平方数,则F(n)=1.其中正确说法的个数是( )
;(3)F(27)=3;(4)若n是一个完全平方数,则F(n)=1.其中正确说法的个数是( )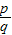 .例如18可以分解成1×18,2×9,3×6这三种,这时就有F(18)=
.例如18可以分解成1×18,2×9,3×6这三种,这时就有F(18)= =
= .给出下列关于F(n)的说法:(1)F(2)=
.给出下列关于F(n)的说法:(1)F(2)= ;(2)F(24)=
;(2)F(24)= ;(3)F(27)=3;(4)若n是一个完全平方数,则F(n)=1.其中正确说法的个数是( )
;(3)F(27)=3;(4)若n是一个完全平方数,则F(n)=1.其中正确说法的个数是( )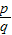 .例如18可以分解成1×18,2×9,3×6这三种,这时就有F(18)=
.例如18可以分解成1×18,2×9,3×6这三种,这时就有F(18)= =
= .给出下列关于F(n)的说法:(1)F(2)=
.给出下列关于F(n)的说法:(1)F(2)= ;(2)F(24)=
;(2)F(24)= ;(3)F(27)=3;(4)若n是一个完全平方数,则F(n)=1.其中正确说法的个数是( )
;(3)F(27)=3;(4)若n是一个完全平方数,则F(n)=1.其中正确说法的个数是( )